Surface Area and Volume of Cuboid
1.घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cuboid),घन और घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cube and Cuboid):
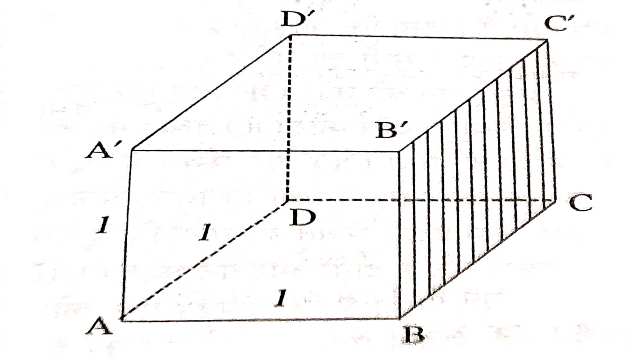
घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cuboid):एक माचिस की डिब्बी,कमरा,चाक का डिब्बा,ईंट आदि घनाभ के उदाहरण हैं।घनाभ को समकोणिक समांतर षट्फलक भी कहा जाता है।आकृति में एक घनाभ दर्शाया है।इसके 6 फलक हैं तथा प्रत्येक फलक एक समतल में आयताकार है।सम्मुख फलक समांतर और सर्वांगसम है।इसमें समांतर फलकों के तीन युग्म है।दो आसन्न फलक एक रेखाखंड पर मिलते हैं जिसे कोर कहते हैं।एक घनाभ में बारह कोरे होती हैं।
तीसरा सलंग्न परस्पर एक दूसरे पर लम्ब हैं।तीन सलंग्न कोरें एक बिंदु पर मिलती है,इसे बिंदु शीर्ष कहते हैं।घनाभ में 8 शीर्ष होते हैं।
आकृति में हम देखते हैं कि AB=A’B’=D’C’=DC=l मान लीजिए
इसी प्रकार AD=A’D’=B’C’=BC=b
और AA’=DD’=CC’=BB’=h
यदि l को घनाभ की लम्बाई,b को घनाभ की चौड़ाई,h को घनाभ की ऊँचाई मान लें तो ये तीनों लाम्बिक संगामी कोरें एक घनाभ को निर्धारित करती हैं।
घनाभ के फलक ABCD का क्षेत्रफल=फलक A’B’C’D’ का क्षेत्रफल=l×h
घनाभ के फलक ADD’A’ का क्षेत्रफल=फलक BCC’B’ का क्षेत्रफल=b×h
घनाभ के फलक ABB’A’ का क्षेत्रफल=फलक DCC’D’ का क्षेत्रफल=b×l
अतः घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल(Total Surface Area of Cubiod)=2(ABCD का क्षेत्रफल+ADD’A’ का क्षेत्रफल+ABB’A’ का क्षेत्रफल)
=2(lb+bh+lh)
=2(lb+bh+lh) वर्ग इकाई
घनाभ की तीनों कोरें अलग-अलग दिशाओं में परस्पर लंबवत हैं।इसलिए घनाभ को त्रिविम आकृति माना जाता है तथा l,b और h लंबाई की इन रेखाओं को घनाभ की भुजाएँ अथवा विमाएं कहा जाता है।ऐसे घनाभ को घनाभ l×b×h भी कहा जाता है।
यदि घनाभ की ऊँचाई (मोटाई अथवा गहराई) शून्य है अर्थात् h=0 तो एक आयत का रूप लेगा।
जब घनाभ की ऊँचाई, चौड़ाई और ऊंचाई समान हैं अर्थात् तो इसे घन कहा जाता है।घन के सभी फलक वर्गाकार होते हैं तथा उसका क्षेत्रफल भी समान होता है।आकृति एक घन को प्रदर्शित करती है।यदि घन की एक भुजा की लंबाई l है तो उसका संपूर्ण पृष्ठीय क्षेत्रफल (Total Surface Area of Cuboid)=2(l×l+l×l+l×l)
=2(l^{2}+l^{2}+l^{2}) \\=2 \times 3 l^{2} \\=6 l^{2} वर्ग इकाई
घनाभ का आयतन (Volume of Cuboid)=lbh घन इकाई
घन का आयतन (Volume of Cube)=l^{3} घन इकाई
घनाभ का विकर्ण (Diagonal of Cuboid)=\sqrt{l^{2}+b^{2}+h^{2}} इकाई
घन के विकर्ण की लम्बाई (Diagonal of Cube)=l \sqrt{3} इकाई
आयतन सम्बन्धी इकाईयाँ
(1.)1 लीटर=1000 घन सेमी
(2.)1 घन सेमी=10×10×10 घन मिमी=1000 घन मिमी
(3.)1 घन मीटर=100×100×100 घन सेमी =100,00,00 घन सेमी
(4.)1 घन मीटर=1000 लीटर=1 किलोलीटर
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Pythagoras Theorem
2.घनाभ का पृष्ठीय क्षेत्रफल और आयतन के उदाहरण (Surface Area and Volume of Cuboid Examples):
Example:1.एक घनाभ 12 सेमी लंबा,9 सेमी चौड़ा और 5 सेमी ऊँचा है।घनाभ का संपूर्ण क्षेत्रफल एवं आयतन ज्ञात कीजिए।
Solution:लम्बाई (l)=12सेमी, चौड़ाई (b)=9 सेमी, ऊँचाई (h)=5 सेमी
घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल=2(lb+bh+lh)
=2(12×9+9×5+5×12) वर्ग सेमी
=2(108+45+60)
=426 वर्ग सेमी
घनाभ का आयतन=lbh
=12×9×5
=540 घन सेमी
Example:2.तीन घनों की भुजाएं क्रमशः 8 सेमी,6 सेमी और 1सेमी हैं इन्हें पिघलाकर एक नया घन बनाया जाता है।नए घन का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:पहले घन की भुजा (a)=8 सेमी
दूसरे घन की भुजा (b)=6 सेमी
तीसरे घन की भुजा (c)=1सेमी
तीनों घनों को मिलाकर एक घन बनाया जाता है।माना इसकी भुजा=x
बड़े का आयतन=तीनों घनों का आयतन
x^{3}=a^{3}+b^{3}+c^{3} \\ \Rightarrow x^{3}=(8)^{3}+6^{3}+1^{3} \\ \Rightarrow x^{3}=512+216+1 \\ \Rightarrow x^{3}=729 \text{ घन सेमी } \\ \Rightarrow x=\sqrt[3]{3 \times 3 \times 3 \times 3 \times 3 \times 3} \\ \Rightarrow x=3 \times 3 =9 \text { सेमी }
बड़े घन का सम्पूर्ण पृष्ठीय क्षेत्रफल=6 \times \text{ ( भुजा) }^2 \\ =6 x^{2} \\ =6 \times(9)^{2} \\ =486\text{ वर्ग सेमी }
Example:3.एक संदूक की माप 50 सेमी×36 सेमी× 25 सेमी है।इस संदूक का कवर बनाने के लिए कितने वर्ग सेमी कपड़े की आवश्यकता होगी?
Solution:सन्दूक की लम्बाई (l)=50 सेमी,चौड़ाई (b)=36 सेमी, ऊँचाई (h)=25 सेमी
सन्दूक का कवर=सन्दूक का सम्पूर्ण पृष्ठीय क्षेत्रफल
=2(lb+bh+lh)
=2[50×36+36×25+25×50] वर्ग सेमी
=2[1800+900+1250] वर्ग सेमी
=2×3950
=7900 वर्ग सेमी
Example:4.एक घन का प्रत्येक पृष्ठ 100 वर्ग सेमी है।यदि आधार के समांतर समतल द्वारा घन को काटकर दो बराबर भागों में बांट दिया जाए तो प्रत्येक समान भाग का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:घन के एक पृष्ठ का क्षेत्रफल (वर्ग)=\text{ ( भुजा) }^2 \\ \text{ ( भुजा ) }^2=100 \\ \Rightarrow \text{ भुजा }=\sqrt{100} \\ \Rightarrow \text{ भुजा }=10 \text{ सेमी }
आधार के समान्तर काटने पर ऊँचाई (h)=\frac{10}{2}=5 \text{ सेमी }
काटने के पश्चात् लम्बाई (l)=10 सेमी
चौड़ाई (b)=10 सेमी
ऊँचाई (h)=5 सेमी
एक भाग का सम्पूर्ण पृष्ठीय क्षेत्रफल=2(lb+bh+lh)
=2(10×10+10×5+5×10) वर्ग सेमी
=2(100+50+50)
=2×200
=400 वर्ग सेमी
Example:5.बगैर ढक्कन का एक बक्सा 3 सेमी मोटी लकड़ी का बना हुआ है।इसकी बाहरी लंबाई 146 सेमी, चौड़ाई 116 सेमी और ऊँचाई 83 सेमी है उसके अंदर की ओर पेन्ट कराने का खर्च ज्ञात कीजिए।पेन्ट की दर ₹2 प्रति 1000 वर्ग सेमी है।
Solution:बक्से में लकड़ी की मोटाई=3 सेमी
बक्से की बाहरी लम्बाई=146 सेमी
बक्से की बाहरी चौड़ाई=116 सेमी
बक्से की बाहरी ऊँचाई=83 सेमी
अन्दर से लम्बाई(l)=146-2×3=146-6=140 सेमी
अन्दर से चौड़ाई (b)=116-2×3=116-6=110 सेमी
अन्दर से ऊँचाई (h)=83-1×3=83-3=80 सेमी
बगैर ढक्कन के बक्से का सम्पूर्ण पृष्ठीय क्षेत्रफल
=2(lb+bh+lh)-bh
=2([140×110+110×80+80×140]-140×110
=2[15400+8800+11200]-15400
=2×35400-15400
=55400 वर्ग सेमी
1000 वर्ग सेमी पर पेन्ट की दर=₹2
1 वर्ग सेमी पर पेन्ट की दर=\frac{2}{1000}
55400 वर्ग सेमी पर पेन्ट का खर्चा=\frac{2}{1000}×55400
=₹118.80
Example:6.एक घनाभ की लम्बाई,चौड़ाई और ऊँचाई का योग 19 सेमी है तथा विकर्ण की लंबाई 11 सेमी है।घनाभ का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:l+b+h=19
विकर्ण=\sqrt{l^{2}+b^{2}+h^{2}}=11\\ \Rightarrow l^{2}+b^{2}+h^{2}=121 \\ \Rightarrow (l+b+h)^{2}= l^{2}+b^{2} +h^{2}+2 \cdot(l b+b h+l h)\\ \Rightarrow (19)^{2}=121+2(l b+b h+l h)\\ \Rightarrow \quad 361-121=2(l b+b h+lh)\\ \Rightarrow 2(l b+b h+l h)=240
घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल=240 वर्ग सेमी
Example:7.6 मीटर भुजा के वर्गाकार फर्श के कमरे में 180 घन मीटर हवा है।कमरे की ऊँचाई ज्ञात कीजिए।
Solution:कमरे का आयतन=हवा का आयतन
lbh=180 घन मीटर
6×6×h=180 [l=6,b=6]
h=\frac{180}{36} \\ \Rightarrow h=5 \text{ मीटर }
Example:8.44 मीटर लंबी,1.5 मीटर ऊंची और 35 सेमी चौड़ी दीवार बनाने में 22 सेमी×10सेमी×7 सेमी माप की कितनी ईटों की आवश्यकता होगी?
Solution:दीवार (घनाभ) का आयतन=lbh
=44 \times 1.5 \times \frac{35}{100} \text{ घन मीटर }
एक ईंट का आयतन=22 \times 10 \times 7 \text{ घन सेमी } \\ =\frac{22 \times 10 \times 7}{1000000} \text{ घन मीटर }
ईटों की संख्या=\frac{\text{ दीवार का आयतन}}{\text{ एक ईंट का आयतन }} \\ \frac{44 \times 1.5 \times 35 \times 1000000}{22 \times 10 \times 7 \times 10}
अतः कुल ईटों की संख्या=15000
Example:9.10 मीटर लंबे,8 मीटर चौड़े और 6 मीटर ऊंचे कमरे में अधिक से अधिक कितनी लंबी छड़ रखी जा सकती है?
Solution:छड़ की अधिकतम लम्बाई=कमरे (घनाभ) का विकर्ण
=\sqrt{l^{2}+b^{2}+h^{2}} \\ =\sqrt{10^{2}+8^{2}+6^{2}} \\ =\sqrt{100+64+36} \\=\sqrt{200} \\=10\sqrt{2} \text{ मीटर }
Example:10.एक घन का आयतन 512घन मीटर है उसकी भुजा ज्ञात करो।
Solution:घन का आयतन=\text{ ( भुजा ) }^3 \\ \text{ ( भुजा ) }^2=512 \text{ घन मीटर } \\ \Rightarrow \text{ भुजा }=\sqrt[3]{512}=\sqrt[3]{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2} \\ \Rightarrow \text{ भुजा }=2 \times 2 \times 2=8 \text{ मीटर }
Example:11.एक दीवार की लंबाई,चौड़ाई और ऊंचाई क्रमशः 5 मीटर,30 सेमी और 3 मीटर है।दीवार बनाने में 20 सेमी×10 सेमी ×7.5 सेमी माप की कितनी ईटों की आवश्यकता है?
Solution:दीवार (घनाभ) का आयतन=lbh
=5 मीटर×30 सेमी×3 मीटर
एक ईंट(घनाभ) का आयतन=lbh
=20 सेमी×10 सेमी ×7.5 सेमी
ईटों की संख्या=\frac{ \text{ दीवार का आयतन}}{\text{ एक ईट का आयतन}} \\ =\frac{ 5 सेमी×30 सेमी×3 मीटर}{20 सेमी×10 सेमी×7.5 सेमी} \\ =\frac{5×100 सेमी×30 सेमी×3×100 सेमी}{20 सेमी×10 सेमी×7.5 सेमी}
=3000 ईटे
Example:12.एक घनाभ की लंबाई,चौड़ाई और ऊंचाई का अनुपात 5:3:2 है।यदि घनाभ का संपूर्ण पृष्ठीय क्षेत्रफल 558 वर्ग सेमी है तो उसकी कोरों का माम ज्ञात कीजिए।
Solution:लम्बाई (l):चौड़ाई (b):ऊँचाई (h)=5:3:2
माना l=5x,b=3x,h=2x
घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल=2(lb+bh+lh)
=2(5x×3x+3x×2x+2x×5x)
\Rightarrow 2\left(15 x^{2}+6 x^{2}+18 x^{2}\right)=558 \\ \Rightarrow 2 \times 31 x^{2}=558 \\ \Rightarrow x^{2}=\frac{558}{2 \times 31}=9 \\ \Rightarrow x=\sqrt{9}=3
अतः लम्बाई(l)=5x=5×3=15 सेमी,चौड़ाई (b)=3x=3×3=9 सेमी, ऊँचाई (h)=2x=2×3=6 सेमी
उपर्युक्त उदाहरणों के द्वारा घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cuboid) को समझ सकते हैं।
3.घनाभ का पृष्ठीय क्षेत्रफल और आयतन की समस्याएं (Surface Area and Volume of Cuboid Problems):
(1.)एक घनाभ 12 सेमी लंबा,9 सेमी चौड़ा और 5 सेमी ऊँचा है।घनाभ का संपूर्ण पृष्ठीय क्षेत्रफल एवं आयतन ज्ञात कीजिए।
(2.)एक घन का संपूर्ण पृष्ठीय क्षेत्रफल 486 वर्ग सेमी है। उसका आयतन ज्ञात कीजिए।
(3.)तीन घनों की भुजाएं क्रमश 8 सेमी,6 सेमी और 1 सेमी है।उन्हें पिघलाकर एक नया घन बनाया गया है।नये घन का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
(4.)यदि एक समकोणिक समान्तर षट्फलक की लम्बाई, चौड़ाई और ऊँचाई का अनुपात 6:5:4 है और उसका सम्पूर्ण पृष्ठीय क्षेत्रफल 333000 वर्ग सेमी है तो समकोणिक समान्तर षट्फलक का आयतन ज्ञात कीजिए।
उत्तर(Answers):(1.)सम्पूर्ण पृष्ठीय क्षेत्रफल=426 वर्ग सेमी, आयतन=540 घन सेमी
(2.)729 घन सेमी
(3.)486 वर्ग सेमी
(4.)405000 घन सेमी
उपर्युक्त सवालों को हल करने पर घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cuboid) को ठीक से समझ सकते हैं।
Also Read This Article:-Properties of Circle
4.घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cuboid),घन और घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cube and Cuboid) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.घनाभ का पृष्ठीय क्षेत्रफल कितना है? (What is the surface area of cuboid?):
उत्तर:एक घनाभ में 6 आयताकार फलक होते हैं।एक घनाभ का पृष्ठीय क्षेत्रफल ज्ञात करने के लिए,सभी 6 फलकों के क्षेत्रफलों को जोड़ें।हम प्रिज्म की लंबाई (l), चौड़ाई (w) और ऊंचाई (h) को भी लेबल कर सकते हैं और पृष्ठीय क्षेत्रफल खोजने के लिए सूत्र, SA=2lw+2lh+2hw का उपयोग कर सकते हैं।
प्रश्न:2.घन और घनाभ का आयतन कितना होता है? (What is volume of cube and cuboid?):
उत्तर:एक घन का आयतन
मूल रूप से,एक घनाभ जिसकी लंबाई,चौड़ाई और ऊंचाई बराबर होती है,घन कहलाता है।चूँकि हम जानते हैं कि घनाभ का आयतन = लंबाई x चौड़ाई x ऊँचाई और घन घनाभ का एक विशेष मामला है जहाँ सभी लंबाई,चौड़ाई और ऊँचाई समान होती है।
अतः घन का आयतन=\text{ भुजा }^3=l^3
प्रश्न:3.पृष्ठीय क्षेत्रफल और आयतन क्या है? (What is the surface area and volume?):
उत्तर:किसी भी वस्तु का पृष्ठीय क्षेत्रफल वस्तु की सतह द्वारा व्याप्त क्षेत्रफल (area) या क्षेत्र (region) होता है।जबकि आयतन किसी वस्तु में उपलब्ध स्थान की मात्रा है अर्थात् उस वस्तु में कितनी मात्रा समा सकती या कितनी यात्रा घेर सकती है।ज्यामिति में,विभिन्न आकार (shapes) और माप (sizes) होते हैं जैसे कि गोला(sphere),घन (cube),घनाभ (cuboid),शंकु (cone),बेलन (cylinder) आदि।प्रत्येक आकृति का अपना पृष्ठीय क्षेत्रफल और साथ ही आयतन होता है।
प्रश्न:4.आप आयतन को पृष्ठीय क्षेत्रफल में कैसे बदलते हैं? (How do you convert volume to surface area?):
उत्तर:पृष्ठीय क्षेत्रफल से आयतन अनुपात कई सरल आकृतियों के लिए आसानी से पाया जा सकता है,उदाहरण के लिए एक घन या एक गोला।एक घन के लिए,पृष्ठीय क्षेत्रफल के लिए समीकरण S=6 l^{2} है,जहाँ L एक भुजा की लंबाई है।इसी प्रकार,घन का आयतन V =l^{3} है।इस प्रकार आयतन के सूत्र द्वारा भुजा ज्ञात करके उसके द्वारा पृष्ठीय क्षेत्रफल ज्ञात किया जा सकता है।
प्रश्न:5.आप घनाभ का आयतन और पृष्ठीय क्षेत्रफल कैसे ज्ञात करते हैं? (How do you find the volume and surface area of a cuboid?):
उत्तर:घनाभ का कुल पृष्ठीय क्षेत्रफल (Total surface area of a cuboid)= 2 [( l × b ) + ( l × h ) + ( b × h )]
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल (Lateral surface area of a cuboid)= 2(l+b)h।
घनाभ का आयतन (Volume of cuboid) (v) = l × b × h
घनाभ के विकर्ण की लंबाई (Length of diagonal of cuboid) = (l² + b² + h²)
घन का आयतन (Volume of cube) = a³
प्रश्न:6.घनाभ के विकर्ण का सूत्र क्या होता है? (What is the formula of diagonal of cuboid?)
उत्तर:प्रयुक्त सूत्र:घनाभ का विकर्ण (Length of diagonal of cuboid) (d)=\sqrt{l^{2}+b^{2}+h^{2}} जहां l घनाभ की लंबाई है,b घनाभ की चौड़ाई है और h घनाभ की ऊंचाई है।
प्रश्न:7.क्यूब और क्यूबॉइड में क्या अंतर है? (What is the difference between cube and cuboid?):
उत्तर:घन और घनाभ के बीच मुख्य अंतर यह है कि एक घन में समान आकार के छह वर्गाकार फलक होते हैं लेकिन एक घनाभ में आयताकार फलक होते हैं।एक घनाभ आयताकार आकार का होता है और एक घन वर्गाकार आकार का होता है।
प्रश्न:8.कुल पृष्ठीय क्षेत्रफल और आयतन में क्या अंतर है? (What is the difference between total surface area and volume?):
उत्तर:पृष्ठीय क्षेत्रफल ठोस आकृति के सभी फलकों के क्षेत्रफलों का योग होता है।ठोस आकृति का पृष्ठीय क्षेत्रफल ज्ञात करना यह पता लगाने जैसा है कि ठोस को ढकने के लिए कितने रैपिंग पेपर की आवश्यकता है;यह बॉक्स के बाहरी फलकों का क्षेत्रफल है।आयतन ठोस आकृति के अंदर की जगह की मात्रा है।
प्रश्न:9.आप पृष्ठीय क्षेत्रफल और आयतन की समस्याओं को आसानी से कैसे हल करते हैं? (How do you solve surface area and volume problems easily?):
उत्तर:आयतन और पृष्ठीय क्षेत्रफल की समस्याओं को हल करने की तरकीबें
घनाभ (Cuboid)।माना लंबाई = l,चौड़ाई = b और ऊँचाई = h इकाई।
घनाभ का पृष्ठीय क्षेत्रफल (Total Surface Area of Cuboid)=2 [( l × b ) + ( l × h ) + ( b × h )]
घनाभ का आयतन (Volume of Cuboid)=l × b × h
घन (Cube)।माना घन के प्रत्येक किनारे की लंबाई a है।
घन का पृष्ठीय क्षेत्रफल (Total Surface Area of Cube)=6 a^{2}
घन का आयतन (Volume of Cube)=a³
सिलेंडर (Cylinder)।माना आधार की त्रिज्या = r और ऊँचाई (या लंबाई) = h।
बेलन का वक्र पृष्ठ का क्षेत्रफल Curved Surface Area of Cylinder)=2 \pi r h
बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल (Total Surface Area of Cylinder)=2 \pi r (h+r)
बेलन का आयतन (Volume of Cylinder)= \pi r^{2} h
शंकु (Cone)।माना आधार की त्रिज्या = r और ऊँचाई = h।
शंकु का वक्र पृष्ठ का क्षेत्रफल Curved Surface Area of Cone)=\pi r l
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल (Total Surface Area of Cone)=\pi r (l+r)
शंकु का आयतन (Volume of Cone)=\frac{1}{3} \pi r^{2} h
गोला।माना गोले की त्रिज्या r है।
गोले का वक्र पृष्ठ का क्षेत्रफल Curved Surface Area of Sphere)=4 \pi r^{2}
गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल (Total Surface Area of Sphere)=4 \pi r^{2}
गोले का आयतन (Volume of Sphere)=\frac{4}{3} \pi r^{3}
अर्द्धगोला (Hemisphere)।
अर्द्धगोला का वक्र पृष्ठ का क्षेत्रफल (Curved Surface Area of Hemisphere)=2 \pi r^{2}
अर्द्धगोला का सम्पूर्ण पृष्ठीय क्षेत्रफल (Total Surface Area of Hemisphere)=3 \pi r^{2}
अर्द्धगोला का आयतन (Volume of Hemisphere)=\frac{2}{3} \pi r^{3}
प्रश्न:10.घनाभ के वक्र पृष्ठीय क्षेत्रफल का सूत्र क्या है? (What is the formula of curved surface area of cuboid?):
उत्तर:घनाभ के कुल पृष्ठीय क्षेत्रफल का सूत्र इस प्रकार दिया गया है, 2 (lb + bh + lh) जहाँ l, b, और h घनाभ की लंबाई,चौड़ाई और ऊँचाई को दर्शाते हैं।
प्रश्न:11.पृष्ठीय क्षेत्रफल और आयतन के बीच तीन प्रमुख अंतर क्या हैं? (What are three major differences between surface area and volume?):
उत्तर:पृष्ठीय क्षेत्रफल एक 2-आयामी अवधारणा है जिसमें इकाइयाँ m², cm² या mm² हैं जबकि आयतन एक 3-आयामी अवधारणा है जिसमें m³, cm³ या mm³ इकाइयों के रूप में हैं।सर्किल,स्क्वायर,आयत जैसे 2-डी आंकड़ों के लिए पृष्ठीय क्षेत्रफल पाया जा सकता है लेकिन उनके लिए वॉल्यूम नहीं पाया जा सकता है।
प्रश्न:12.सम्पूर्ण पृष्ठीय क्षेत्रफल और वक्र पृष्ठीय क्षेत्रफल में क्या अंतर है? (What is the difference between total surface area and curved surface area?):
उत्तर:सबसे पहले इसका जवाब दिया गया:कुल पृष्ठीय क्षेत्रफल और वक्र पृष्ठीय क्षेत्रफल में क्या अंतर है? एक सिलेंडर के मामले में,कुल पृष्ठीय क्षेत्रफल में सिलेंडर के दो छोर शामिल होते हैं जो गोलाकार समतल होते हैं जबकि वक्र पृष्ठीय क्षेत्रफल में सिलेंडर सतह की वक्रता के साथ क्षेत्रफल होता है।यानि समतल गोलाकार सतहो,जो छोर पर स्थित होते हैं का क्षेत्रफल शामिल नहीं होता है।
सम्पूर्ण पृष्ठीय क्षेत्रफल में सभी फलकों का क्षेत्रफल सम्मिलित होता है जबकि वक्र पृष्ठ के क्षेत्रफल में ठोस के वक्र भाग क्षेत्रफल शामिल होता है।
प्रश्न:13.क्षेत्रफल और आयतन में क्या अंतर है? (What are differences between area and volume?):
उत्तर:क्षेत्रफल एक समतल में द्वि-आयामी समतल वस्तु द्वारा व्याप्त स्थान की मात्रा है।आयतन को त्रि-आयामी वस्तु के कब्जे वाले स्थान के रूप में परिभाषित किया गया है।क्षेत्रफल को हमेशा वर्ग इकाइयों में मापा जाता है।आयतन को हमेशा घन इकाइयों में मापा जाता है।
प्रश्न:14.आकार और आयतन में क्या अंतर है? (What is the difference between shape and volume?):
उत्तर:आकार दो-आयामी अंतरिक्ष में एक क्षेत्र को संदर्भित करता है जिसे किनारों द्वारा परिभाषित किया जाता है; आयतन त्रि-आयामी है,जो ऊँचाई,चौड़ाई और गहराई को प्रदर्शित करता है।
प्रश्न:15.आयतन और पृष्ठीय क्षेत्रफल क्यों महत्वपूर्ण है? (Why is volume and surface area important?):
उत्तर:महत्वपूर्ण बात यह है कि जैसे-जैसे सेल बड़ा होता जाता है,सतह का आयतन अनुपात छोटा होता जाता है। इस प्रकार,यदि कोशिका एक निश्चित सीमा से आगे बढ़ती है, तो पर्याप्त सामग्री झिल्ली को इतनी तेजी से पार करने में सक्षम नहीं होगी कि बढ़ी हुई सेलुलर मात्रा को समायोजित कर सके।इसलिए कोशिकाएँ इतनी छोटी होती हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cuboid),घन और घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cube and Cuboid) के बारे में ओर अधिक जानकारी प्राप्त कर सकते है।
उपर्युक्त प्रश्नों के उत्तर द्वारा घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cuboid),घन और घनाभ का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cube and Cuboid) के बारे में ओर अधिक जानकारी प्राप्त कर सकते है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
