Equation of Line Passing Through Point
1.दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point),दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा का समीकरण (Equation of line passing through given point and making certain angle with given line)-
इस आर्टिकल में दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point),दो रेखाओं के मध्य कोण,दो रेखाओं के समान्तर होने के लिए आवश्यक प्रतिबन्ध,दो रेखाओं के परस्पर लम्बवत् होने का प्रतिबन्ध के बारे में अध्ययन करेंगे।
यहां दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण से अर्थ यह है कि दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा का समीकरण से है।
(1.)दो रेखाओं के मध्य कोण (Angle Between Two Lines)-
दो रेखाओं के मध्य कोण \phi=\tan ^{-1}\left[\pm \frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\right]
दोनों रेखाओं के मध्य कोण न्यूनकोण है तब \frac{m_{1}-m_{2}}{1+m_{1} m_{2}} धनात्मक लेते हैं।जब अधिक कोण हो तब यह राशि ऋणात्मक लेते हैं।
(2.)दो रेखाओं के समान्तर होने के लिए आवश्यक प्रतिबन्ध (Necessary Condition for Lines to be Parallel)-
m_{1}=m_{2}
(3.)दो रेखाओं के परस्पर लम्बवत् होने का प्रतिबन्ध (Condition for Two Lines to be Mutually Perpendicular)-
m_{1} m_{2}=-1
(4.)दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा की समीकरण (Equation of Line Passing Through Given Point and Making Certain Angle With Given Line)-
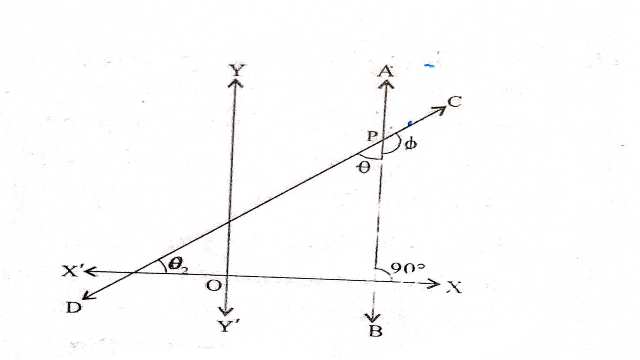
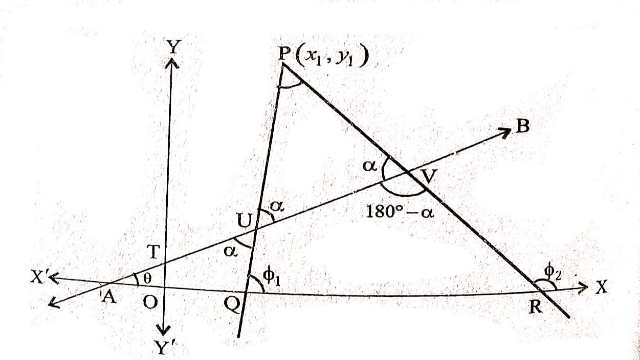
माना कि कोई बिन्दु (x_{1},y_{1}) है तथा AB कोई रेखा है जो x-अक्ष के साथ \theta कोण बनाती है तथा P से गुजरने वाली दो अभीष्ट रेखाएं PQ,PR, x-अक्ष से क्रमशः {\phi}_{1} तथा {\phi}_{2} कोण बनाती है।
PQ का समीकरण y-y_{1}=\tan \phi_{1} \cdot\left(x-x_{1}\right) \cdots (1)
तथा PR का समीकरण y-y_{1}=\tan \phi_{2}\left(x-x_{1}\right) \cdots(2)
अब दी गई रेखा AB का समीकरण
y=m x+c(\because m=\tan \theta, O T=c)
जो कि PQ तथा PR से \alpha कोण बनाती है।
\triangle AUQ तथा \triangle AVR में
\phi_{1}=\theta+\alpha और \phi_{2}=\theta+(180-\alpha)
अतः \tan \phi_{1}=\tan (\theta+\alpha) \\ \Rightarrow \quad \tan \phi_{1} =\frac{\tan \theta+\tan \alpha}{1-\tan \theta \tan \alpha} \\ \Rightarrow \tan \phi_{1} =\frac{m+\tan \alpha}{1-m \tan \alpha} ....(3) \\ \Rightarrow \tan \phi_{2} =\tan \left[\theta+\left(180^{\circ}-\alpha\right)\right] \\ =\tan \left[180^{\circ}+(\theta-\alpha)\right]
अतः \tan \phi_{2} =\tan (\theta-\alpha) \\ =\frac{\tan \theta-\tan \alpha}{1+\tan \theta \tan \alpha} \\ \Rightarrow \tan \phi_{2} =\frac{m-\tan \alpha}{1+m \tan \alpha} \cdots(4)
\tan \phi_{1} तथा \tan \phi_{2} का मान समीकरण (3) तथा (4) से समीकरण (1) और (2) में रखने पर अभीष्ट रेखा का समीकरण प्राप्त होता है-
y-y_{1} =\frac{m+\tan \alpha}{1-m \tan \alpha}\left(x-x_{1}\right) \cdots(5) \\ \Rightarrow y-y_{1} =\frac{m-\tan \alpha}{1+m \tan \alpha}\left(x-x_{1}\right)\cdots (6)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Line Passing Through Two Points Equation
2.दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण के उदाहरण (Equation of Line Passing Through Point Examples)-
Example-1.निम्नलिखित सरल रेखाओं के मध्य का कोण ज्ञात कीजिए
\frac{x}{a}+\frac{y}{b}=1 तथा \frac{x}{b}-\frac{y}{a}=1
Solution–\frac{x}{a}+\frac{y}{b}=1 \\ m_{1}=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ =-\frac{(\frac{1}{a})}{(\frac{1}{b})} \\ \Rightarrow m_{1}=-\frac{b}{a} \\ \frac{x}{b}-\frac{y}{a}=1 \\m_{2}=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ =-\frac{(\frac{1}{b})}{(-\frac{1}{a})} \\ \Rightarrow m_{2}=\left(\frac{a}{b}\right) \\ \tan \theta =\frac{m_{1}-m_{2}}{1+m_{2} m_{2}} \\ =\frac{-\frac{b}{a}-\frac{a}{b}}{1+\frac{-b}{a} \cdot \frac{a}{b}} \\ =\frac{-\frac{\left(b^{2} +a^{2}\right)}{a b}}{1-1} \\ =-\infty \\ \tan \theta=\tan \frac{\pi}{2} \\ \Rightarrow \theta=90^{\circ}
Example-2.सिद्ध कीजिए कि निम्नलिखित सरल रेखाएं समान्तर हैं x \cos \alpha+y \sin \alpha=p तथा x+y \tan \alpha=5 \tan \alpha
Solution–x \cos \alpha+y \sin \alpha=p \\ m_{1}=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ =-\frac{\cos \alpha}{\sin \alpha} \\ \Rightarrow m_{1} =-\cot \alpha \\ x+y \tan \alpha=5 \tan \alpha \\ m_{2}=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ \Rightarrow m_{2}=-\frac{1}{\tan \alpha} \\ \Rightarrow m_{2}=-\cot \alpha \\ \Rightarrow m_{1}=m_{2}
अतः सरल रेखाएं समान्तर हैं।
Example-3.सिद्ध कीजिए कि रेखाएं जिनके समीकरण 4x+5y+7=0 तथा 5x-4y-11=0 है परस्पर लम्बवत् हैं।
Solution-4x+5y+7=0
m_{1}=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ \Rightarrow m_{1}=-\left(\frac{4}{5}\right)
5x-4y-11=0
m_{2}=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ =-\frac{5}{(-4)} \\ \Rightarrow m_{2}=\frac{5}{4} \\ m_{1} m_{2}=-\left(\frac{4}{5}\right) \times\left(\frac{5}{4}\right) \\ \Rightarrow m_{1} m_{2}=-1
उन सरल रेखाओं के समीकरण ज्ञात कीजिए जो-
Example-4.रेखा 2x+5y=7 के समान्तर है तथा बिन्दुओं (2,7) तथा (-4,1) को मिलाने वाली रेखा के मध्य बिन्दु से होकर जाती है।
Solution– 2x+5y=7
m=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ \Rightarrow m=-\frac{2}{5}
(2,7) तथा (-4,1) का मध्य बिन्दु=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right) \\ =\left(\frac{2-4}{2}, \frac{7+1}{2}\right)
=(-1,4)
अतः (-1,4) से गुजरने वाली रेखा का समीकरण-
y-y_{1}=m\left(x-x_{1}\right) \\ y-4=(-\frac{2}{5})(x+1) \\ 5y-20=-2x-2 \\ \Rightarrow 2x+5y=18
Example-5.बिन्दुओं (-3,7) तथा (5,-4) को मिलाने वाले रेखाखण्ड को 4:7 के अनुपात में विभाजित करती है तथा इस पर लम्ब है।
Solution-(-3,7) तथा (5,-4) से गुजरने वाली रेखा की प्रवणता
m_{1} =\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{-4-7}{5+3} \\ =-\frac{11}{8}
लम्बवत् रेखा की प्रवणता m=m_{2}=-\frac{1}{m_{1}} \\ m=\frac{8}{11}
(-3,7) तथा (5,-4) को 4:7 के अनुपात में विभाजित करने वाले बिन्दु के निर्देशांक
x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ =\frac{4(5)+7(-3)}{4+7} \\ =\frac{20-21}{11} \\ x=-\frac{1}{11} \\ y =\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ =\frac{4(-4)+7(7)}{4+7} \\ =\frac{-16+49}{11} \\ =\frac{33}{11} \\ \Rightarrow y =3
अतः (-\frac{1}{11},3) से गुजरने वाली रेखा की समीकरण
y-y_{1}=m\left(x-x_{1}\right) \\ \Rightarrow y-3=\frac{8}{11}\left(x+\frac{1}{11}\right) \\ \Rightarrow 121 y-363=88 x+8 \\ \Rightarrow 88 x-121 y+371=0
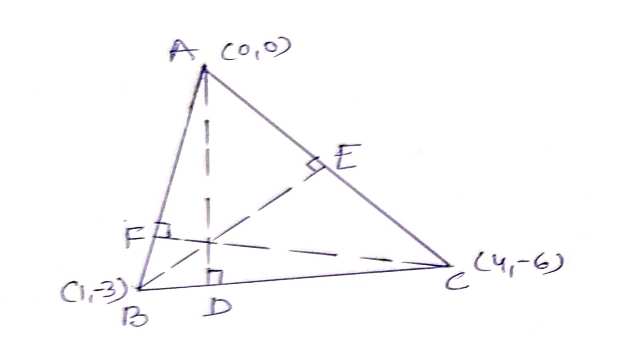
Example-6.एक त्रिभुज के शीर्ष (0,0),(4,-6) और (1,-3) हैं,इन बिन्दुओं से त्रिभुज के सम्मुख भुजाओं पर डाले गए लम्बों के समीकरण ज्ञात कीजिए।
Solution-B(1,-3),C(4,-6)
BC की प्रवणता m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =-\frac{6+3}{4-1} \\ =-\frac{3}{3} \\ m =-1
अतः AD की समीकरण जो (0,0) से गुजरती है तथा BC के लम्बवत् है
y-y_{1}=-\frac{1}{m}\left(x-x_{1}\right) \\ \Rightarrow y-0=-\frac{1}{(-1)}(x-0) \\ \Rightarrow y=x \Rightarrow y-x=0
A(0,0),C(4,-6)
AC की प्रवणता m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{-6-0}{4-0} \\ m =-\frac{3}{2}
अतः BE की समीकरण जो (1,-3) से गुजरती है तथा AC के लम्बवत् है
y-y_{1}=-\frac{1}{m}\left(x-x_{1}\right) \\ \Rightarrow y+3=-\frac{1}{(-\frac{3}{2})}(x-1) \\ \Rightarrow y+3=\frac{2}{3}(x-1) \\ \Rightarrow 3 y+9=2 x-2 \\ \Rightarrow 2 x-3 y=11
A(0,0),B(1,-3)
AB की प्रवणता m =\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{-3-0}{1-0} \\ m =-3
अतः CF की समीकरण जो (4,-6) से गुजरती है तथा AB के लम्बवत् है-
y-y_{1}=-\frac{1}{m}\left(x-x_{1}\right) \\ \Rightarrow y+6=-\frac{1}{(-3)}(x-4) \\ \Rightarrow y+6=\frac{1}{3}(x-4) \\ \Rightarrow 3 y+18=x-4 \\ \Rightarrow x-3 y=22
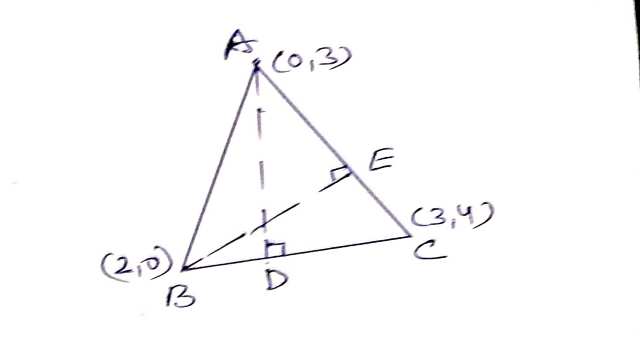
Example-7.उस त्रिभुज का लम्बकेन्द्र ज्ञात कीजिए जिसके शीर्ष (2,0),(3,4) और (0,3) हैं।
Solution-B(2,0),C(3,4)
BC की प्रवणता m =\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{4-0}{3-2} \\ m =4
AD की समीकरण जो (0,3) से गुजरती है तथा BC के लम्बवत् है-
y-y_{1}=-\frac{1}{m}\left(x-x_{1}\right) \\ \Rightarrow y-3=-\frac{1}{4}(x-0) \\ \Rightarrow 4 y-12=-x \\ \Rightarrow x+4 y=12 \cdots(1)
A(0,3),C(3,4)
AC की प्रवणता
m =\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{4-3}{3-0} \\ m =\frac{1}{3}
अतः BE की समीकरण जो (2,0) से गुजरती है तथा AC के लम्बवत् है
y-y_{1}=-\frac{1}{m}\left(x-x_{1}\right) \\ \Rightarrow y-0=-\frac{1}{(\frac{1}{3})}(x-2) \\ \Rightarrow y=-3(x-2) \\ \Rightarrow y=-3 x+6 \\ \Rightarrow 3 x+y=6 \cdots(2) \\ x+4 y=12 \cdots(1)
समीकरण (1) तथा (2) को हल करने पर-
y=\frac{30}{11}, x=\frac{12}{11}
अतः लम्बकेन्द्र के निर्देशांक (\frac{12}{11},\frac{30}{11})
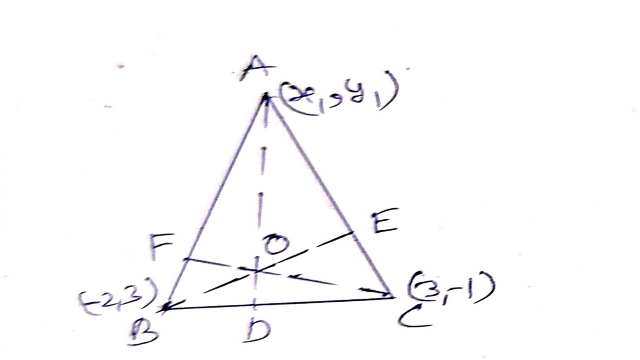
Example-8.किसी त्रिभुज के दो शीर्ष (3,-1) तथा (-2,3) है। त्रिभुज का लम्बकेन्द्र मूलबिन्दु पर है। तीसरे शीर्ष के निर्देशांक ज्ञात कीजिए।
Solution-माना तीसरे शीर्ष के निर्देशांक A(x_{1},y_{1}) हैं।
A(x_{1},y_{1}),(0,0)
AD की प्रवणता m_{1} =\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{0-y_{1}}{0-x_{1}} \\ m_{1} =\frac{y_{1}}{x_{1}}
B(-2,3),C(3,-1)
BC की प्रवणता m_{2} =\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{-1-3}{3+2} \\ =-\frac{4}{5}
AD तथा BC लम्बवत् हैं अतः लम्बवत् होने का प्रतिबंध
m_{1} m_{2}=-1 \\ \left(\frac{y_{1}}{x_{1}}\right)\left(-\frac{4}{5}\right)=-1 \\ \Rightarrow 4 y_{1}=5 x_{1} \\ 5 x_{1}-4 y_{1}=0 \cdots (1)
A(x_{1},y_{1}),C(3,-1)
AC की प्रवणता
m_{1}=\frac{-1-y_{1}}{3-x_{1}} \\ m_{1}=-\left(\frac{1+y_{1}}{3-x_{1}}\right)
BE की प्रवणता
m_{2}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{0-3}{0+2} \\ \Rightarrow m_{2}=-\frac{3}{2}
BE तथा AC लम्बवत् हैं अतः लम्बवत् होने का प्रतिबन्ध
m_{1} m_{2}=-1 \\ \Rightarrow-\left(\frac{1+y_{1}}{3-x_{1}}\right)\left(-\frac{3}{2}\right)=-1 \\ \Rightarrow 3\left(1+y_{1}\right)=-2\left(3-x_{1}\right) \\ \Rightarrow 3+3 y_{1}=-6+2 x_{1} \\ \Rightarrow 2 x_{1}-3 y_{1}=9 \cdots (2)
समीकरण (1) को 2 से तथा समीकरण (2) को 5 से गुणा करने पर-
10 x_{1}-8 y_{1}=0 \cdots(3) \\ 10 x_{1}+15 y_{1}=45 \cdots(4) \\................................ \text { घटाने पर } \\ 7 y_{1}=-45 \\ y_{1}=-\frac{45}{7}
y_{1} का मान समीकरण (1) में रखने पर-
5 x_{1}-4\left(-\frac{45}{7}\right)=0 \\ \Rightarrow 5 x_{1}=-\frac{225}{7} \\ \Rightarrow x_{1}=-\frac{36}{7}
अतः त्रिभुज के तीसरे शीर्ष के निर्देशांक \left(-\frac{36}{7},-\frac{45}{7}\right)
Example-9.बिन्दुओं (2,-3) तथा (1,-5) को मिलाने वाले रेखाखण्ड के लम्बअर्द्धक का समीकरण ज्ञात कीजिए।
Solution-A(2,-3) तथा B(1,-5) का मध्य बिन्दु है-
\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right) \\ =\left(\frac{2+1}{2},-\frac{-3-5}{2}\right) \\ =\left(\frac{3}{2},-4\right)
AB की प्रवणता m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ =\frac{-5+3}{1-2} \\ =\frac{-2}{-1} \\ m =2
AB के लम्बअर्द्धक की प्रवणता =-\frac{1}{m}
AB के लम्बअर्द्धक की समीकरण जो (\frac{3}{2},-4 ) से गुजरती है-
y-y_{1}=-\frac{1}{m}\left(x-x_{1}\right) \\ \Rightarrow y+4=-\frac{1}{2}\left(x-\frac{3}{2}\right) \\ \Rightarrow 2 y+8=-x+\frac{3}{2} \\ \Rightarrow 4 y+16=-2 x+3 \\ \Rightarrow 2 x+4 y+13=0
Example-10.उस रेखा का समीकरण ज्ञात कीजिए जो सरल रेखा पर \frac{x}{a}-\frac{y}{b}=1 ,उस बिन्दु जहां वह x-अक्ष से मिलती है,लम्ब है।
Solution–\frac{x}{a}-\frac{y}{b}=1 सरलरेखा x-अक्ष पर मिलती है अतःy=0
\frac{x}{a}=1 \Rightarrow x=a
अतः x-अक्ष पर बिन्दु के निर्देशांक जहां वह रेखा से मिलती है (a,0)
\frac{x}{a}-\frac{y}{b}=1 की प्रवणता
m=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ =-\frac{(\frac{1}{a})}{(-\frac{1}{b})} \\ \Rightarrow m=\left(\frac{b}{a}\right)
लम्बरेखा की प्रवणता=-\frac{1}{m}
अतः लम्बरेखा की समीकरण जो (a,0) से गुजरती है-
y-y_{1}=-\frac{1}{m}\left(x-x_{1}\right) \\ \Rightarrow y-0=-\frac{1}{\left(\frac{b}{a}\right)}(x-a) \\ \Rightarrow y=-\frac{a}{b}(x-a) \\ \Rightarrow b y=-a x+a^{2} \\ \Rightarrow a x+b y=a^{2}
Example-11.उन सरल रेखाओं के समीकरण ज्ञात कीजिए जो (2,-3) से गुजरती है तथा सरलरेखा 3x-2y=4 से 45° का कोण बनाती है।
Solution-एक दिए हुए बिन्दु x_{1},y_{1} से गुजरने वाली तथा एक दी हुई रेखा y=mx+c के साथ दिया गया कोण \alpha बनाने वाली रेखाओं का समीकरण
y-y_{1}=\frac{m+\tan \alpha}{1-m \tan \alpha}\left(x-x_{1}\right) \cdots(1)
तथा y-y_{1}=\frac{m-\tan \alpha}{1+m \tan \alpha}\left(x-x_{1}\right) \cdots(2)
प्रश्नानुसार (x_{1},y_{1})=(2,-3) ; \alpha=45^{\circ} \Rightarrow \tan \alpha=\tan 45^{\circ}=1
रेखा 3x-2y=4 की प्रवणता
m=-\frac{\text{ x का गुणांक } }{\text{ y का गुणांक }} \\ =-\frac{3}{-2} \\ m=\frac{3}{2}
ये मान समीकरण (1) व (2) में रखने पर अभीष्ट रेखाओं के समीकरण-
y+3=\frac{\frac{3}{2}+1}{1-\frac{3}{2}(1)}(x-2) \\ \Rightarrow y+3=\frac{\frac{3}{2}}{-\frac{1}{2}}(x-2) \\ \Rightarrow y+3=-5(x-2) \\ \Rightarrow 5 x+y=7 \\ y+3=\frac{\frac{3}{2}-1}{1+\frac{3}{2}}(x-2) \\ \Rightarrow y+3=\frac{\frac{1}{2}}{\frac{5}{2}}(x-2) \\ \Rightarrow y+3=\frac{1}{5}(x-2) \\ \Rightarrow 5 y+15=x-2
x-5y=17 तथा 5x+y=7
Example-12.उन रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (4,5) से गुजरती है तथा रेखाओं 3x=4y+7 और 5y=12x+6 से समान कोण बनाती है।
Solution– 3x=4y+7 की प्रवणता m=\frac{3}{4} तथा रेखा 5y=12x+6 की प्रवणता m=\frac{12}{5}
\tan \phi_{1}=\frac{m-\tan \alpha}{1+m \tan \alpha} \\ \Rightarrow \frac{\frac{3}{4}-\tan \alpha}{1+\frac{3}{4} \tan \alpha}=\pm \frac{\frac{12}{5}-\tan \alpha}{1+\frac{12}{5} \tan 2}\\ \Rightarrow \frac{3-4 \tan \alpha}{4+3 \tan \alpha}=\frac{12-5 \tan \alpha}{5+12 \tan \alpha}
धनात्मक चिन्ह लेने पर-
\Rightarrow 15+16 \tan \alpha-48 \tan ^{2} \alpha=48+16 \tan 2-15 \tan ^{2} \alpha \\ \Rightarrow -33 \tan ^{2} \alpha=33 \\ \Rightarrow \tan ^{2} \alpha=-1 \Rightarrow \tan ^{2} \alpha=\sqrt{-1}
जो कि असम्भव है।ऋणात्मक चिन्ह लेने पर-
\Rightarrow \frac{3-4 \tan \alpha}{4+3 \text { tome }}=-\frac{(12-5 \tan \alpha)}{5+12 \tan \alpha} \\ \Rightarrow 15+16 \tan \alpha-48 \tan ^{2} \alpha=-48-16 \tan \alpha+15 \tan ^{2} \alpha \\ \Rightarrow 63 \tan ^{2} \alpha-32 \tan \alpha-63=0 \\ \Rightarrow \quad 63 \tan ^{2} \alpha-81 \tan \alpha+49 \tan 2-63=0 \\ \Rightarrow 9 \tan \alpha(7 \tan \alpha-9)+7(7 \tan \alpha-9)=0 \\ \Rightarrow(9 \tan \alpha+7)(7 \tan \alpha-9)=0 \\ \Rightarrow \tan 2=-\frac{7}{9}, \frac{9}{7}
अतः (4,5) से गुजरने वाली तथा उपर्युक्त प्रवणता वाली रेखाओं के समीकरण-
y-5=-\frac{7}{9}(x-4) \\ \Rightarrow 9 y-45=-7 x+28 \\ \Rightarrow 7 x+9 y=73 \\ y-5=\frac{9}{7}(x-4) \\ \Rightarrow 7 y-35=9 x-36 \\ \Rightarrow 9 x-7 y=1
उपर्युक्त उदाहरणों के द्वारा दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point),दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा का समीकरण (Equation of line passing through given point and making certain angle with given line) को समझ सकते हैं।
3.दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण के उदाहरण (Equation of Line Passing Through Point Examples)-
(1.) रेखाओं 2y-3x+5=0 तथा 4x+5y+8=0 के बीच का कोण ज्ञात करो।
(2.) सिद्ध कीजिए कि रेखाएं 2y=mx+c तथा 4y=2mx समान्तर हैं।
उन सरल रेखाओं के समीकरण ज्ञात कीजिए जो
(3.)बिन्दु (4,5) से गुजरती है तथा 2x-3y-5=0 रेखा के समान्तर हैं।
(4.)बिन्दु (1,2) से गुजरती है तथा रेखा 4x+3y+8=0 के लम्बवत् हैं।
(5.)उस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखा 2x+3y+11=0 के समान्तर हैं तथा अक्षों पर काटे गए अन्त: खण्डों का योग 15 है।
उत्तर (Answers):(1) \tan ^{-1}\left(-\frac{23}{2}\right)
(3.)2x-3y+7=0
(4.)3x-4y+5=0
(5.)2x+3y-18=0
उपर्युक्त सवालों को हल करने पर दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point),दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा का समीकरण (Equation of line passing through given point and making certain angle with given line) को ठीक से समझ सकते हैं।
Also Read This Article:-Equation of Straight Lines
4.दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न-
प्रश्न:1.आप एक रेखा के समीकरण को कैसे ज्ञात करते हैं जो एक बिंदु से गुजरता है और एक रेखा के लंबवत है? (How do you Find the Equation of a Line that Passes Through a Point and is Perpendicular to a Line?)
उत्तर-y-y_{1} =m (x-x_{1}) से एक बिन्दु से गुजरने वाली रेखा का समीकरण ज्ञात किया जा सकता है इसलिए इस रेखा की प्रवणता (ढ़ाल) m है।लंबवत रेखा की ढ़ाल (-\frac{1}{m}) होती हैं,इसलिए जिस सरलरेखा को हम ज्ञात करना चाहते हैं उसका समीकरण होगा-
y-y_{1} =-\frac{1}{m} (x-x_{1})
यदि y अन्त:खण्ड अर्थात् c का मान दिया हुआ हो तो रेखा y=mx+c के लम्बवत् रेखा का समीकरण होगा-
y=(-\frac{1}{m})x+c
प्रश्न:2.उस रेखा का समीकरण क्या है जो बिन्दु \frac{1}{3} और -\frac{2}{5} से होकर गुजरती है? (What is the Equation of a Line that Passes Through the Points \frac{1}{3} and (-\frac{2}{5})?)
उत्तर-बिन्दु ( \frac{1}{3},-\frac{2}{5}) से गुजरने वाली रेखा का समीकरण होगा-
y-(-\frac{2}{5})=m(x-\frac{1}{3})
प्रश्न:3.आपको दो बिंदुओं से गुजरने वाली रेखा का समीकरण कैसे ज्ञात करते है? (How do you Find the Equation of a Line that Passes Through Two Points?)
उत्तर-दो बिन्दुओं (x_{1},y_{1}) तथा (x_{2},y_{2}) से गुजरने वाली रेखा का समीकरण होगा-
y-y_{1} =m (x-x_{1})
प्रवणता (ढ़ाल) m का मान निम्न सूत्र द्वारा ज्ञात किया जाएगा-
m=\frac{(y_{2}-y_{1})}{(x_{2}-x_{1})}
प्रश्न:4.एक बिंदु से गुजरने वाली सरल रेखा का समीकरण (Equation of a Straight Line Passing Through a point),एक बिंदु के साथ एक रेखा का समीकरण कैसे ज्ञात करें? (How to Find the Equation of a Line with one Point?)
उत्तर-यदि एक बिन्दु तथा प्रवणता (ढ़ाल) m का मान दिया गया हो तो निम्न सूत्र द्वारा सरलरेखा का समीकरण ज्ञात किया जा सकता है-
y-y_{1} =m (x-x_{1})
यदि y अन्त:खण्ड अर्थात् c का मान तथा एक बिन्दु दिया हो तो निम्न सूत्र से सरलरेखा का समीकरण ज्ञात किया जाता है-
y=mx+c
हम एक सरल रेखा y = mx + c के व्यापक समीकरण से शुरू करते हैं।यह तब बिंदु (x_{1},y_{1}) से गुजरते हुए प्रवणता (ढ़ाल) m के साथ एक सरल रेखा का प्रतिनिधित्व करता है।तो यह व्यापक रूप उपयोगी है यदि आप रेखा पर ढाल और एक बिंदु जानते हैं।
प्रश्न:5. दो बिंदुओं से गुजरने वाली सरल रेखा का समीकरण (Equation of Straight Line Passing Through Two Points),दो बिंदुओं से दी गई रेखा के समीकरण का पता लगाना (Finding the Equation of a Line Given Two Points)
उत्तर-दो बिन्दुओं से गुजरने वाली रेखा का समीकरण ज्ञात करने के लिए निम्न समीकरण का प्रयोग किया जाता है-
y-y_{1} =m (x-x_{1})
प्रवणता अर्थात् ढ़ाल m का मान निम्न सूत्र द्वारा ज्ञात किया जाता है-
m=\frac{(y_{2}-y_{1})}{(x_{2}-x_{1})}
उपर्युक्त प्रश्नों के उत्तर द्वारा दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point),दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा का समीकरण (Equation of line passing through given point and making certain angle with given line) को भली-भांति समझ सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point),दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा का समीकरण (Equation of line passing through given point and making certain angle with given line) को भली-भांति समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |