Motion Under Central Force
1.केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole)-
केन्द्रीय बल के अधीन गति (Motion Under Central Force) ज्ञात करने के लिए केन्द्रीय बल,सकेन्द्र कक्षा को जानना आवश्यक है।
केन्द्रीय बल (Central Force)-जब एक कण किसी ऐसे बल के अधीन गमन करता है जिसकी दिशा सर्वदा एक नियत बिन्दु की ओर होती है तो वह बल केन्द्रीय बल कहलाता है और नियत बिन्दु बल का केन्द्र कहलाता है।
सकेन्द्र कक्षा (Central Orbit)-किसी केन्द्रीय बल के प्रभाव के अधीन चलने वाले किसी कण की गति के पथ को सकेन्द्र कक्षा कहते हैं।
एक कण एक ऐसे त्वरण सहित समतल में गतिमान है जिसकी दिशा सर्वदा समतल में एक स्थिर बिन्दु (नियत) बिन्दु की ओर रहती है,उसके पथ का अवकल समीकरण ज्ञात करना।
(A particle moves in a plane with an acceleration which is always directed to a fixed point O in the plane; to obtain the differential equation of its path.)
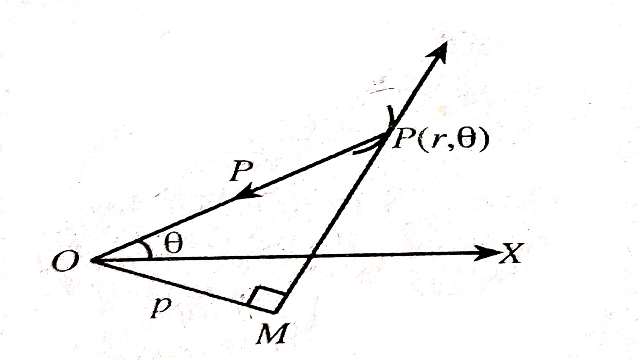
व्युत्क्रम ध्रुवीय रूप (Reciprocal polar form)-माना कि O एक नियत बिन्दु है,O को मूलबिन्दु तथा इससे गुजरने वाली किसी स्थिर रेखा OX को प्रारम्भिक रेखा लेकर,माना कि किसी समय t पर कण बिन्दु P पर है जिसके ध्रुवी निर्देशांक (r, \theta) हैं।
चूंकि कण की त्वरण की दिशा सर्वदा नियत बिन्दु O की ओर है इसलिए कण का केवल अरीय (radial) त्वरण होगा तथा अनुप्रस्थ (Transverse) त्वरण शून्य होगा।
माना कि त्वरण बिन्दु O की ओर p है,तब कण की अरीय एवं अनुप्रस्थ गति समीकरण:
\ddot{r}-r {\dot{\theta}}^{2}=-P \cdots(1)
तथा \frac{1}{r} \frac{d}{d t}\left(r^{2} \frac{d \theta}{d t}\right)=0 \cdots(2)
(2) का समाकलन करने पर-
r^{2}\left(\frac{d \theta}{d t}\right)=अचर=h (माना)…..(3)
अब यदि r=\frac{1}{u} तब इसका t के सापेक्ष अवकलन करने पर-
\frac{d r}{d t} =\left(-\frac{1}{u^{2}}\right) \frac{d u}{d t} \\ =\left(-\frac{1}{u^{2}}\right)\left(\frac{d u}{d \theta}\right)\left(\frac{d \theta}{d t}\right) \\ =\left(-\frac{1}{u^{2}}\right)\left(\frac{d u}{d \theta}\right)\left(\frac{h}{r^{2}}\right) [समीकरण (3) से]
\Rightarrow \frac{dr}{d t}=(-h) \frac{d u}{d \theta}\left[\because r=\frac{1}{u}\right] \cdots(4)
अतः t के सापेक्ष अवकलन करने पर-
\frac{d^{2} r}{d t^{2}} =(-h) \frac{d}{d t}\left(\frac{d u}{d \theta}\right) \\ =-h\left(\frac{d^{2} u}{d \theta^{2}}\right) \cdot\left(\frac{d \theta}{d t}\right) \\ =-h\left(\frac{d^{2} u}{d \theta^{2}} \right)\left(\frac{h}{r^{2}}\right) [समीकरण (3) से]
\Rightarrow \frac{d^{2} r}{d t^{2}}=-h^{2} u^{2}\left(\frac{d^{2} u}{d \theta^{2}}\right) \cdots(5)
अब \left(\frac{d^{2} r}{d t^{2}}\right) तथा \left(\frac{d \theta}{d t}\right) के मान क्रमशः (5) तथा (3) से (1) में प्रतिस्थापित करने पर-
-h^{2} u^{2}\left(\frac{d^{2} u}{d \theta^{2}}\right)-r \cdot\left(\frac{h^{2}}{r^{4}}\right)=-P \\ \Rightarrow-h^{2} u^{2}\left(\frac{d^{2} u}{d \theta^{2}}\right)-h^{2} u^{2}=-P \\ \Rightarrow \quad h^{2} u^{2}\left(u+\frac{d^{2} u}{d \theta^{2}}\right)=P \cdots (6)
यह सकेन्द्र कक्षा का अभीष्ट व्युत्क्रम ध्रुवीय निर्देशांकों में अवकल समीकरण है।
पदिक रूप में सकेन्द्र कक्षा का अवकल समीकरण ज्ञात करना:
(To find the differential equation of a central orbit in pedal form.):
हम अवकल गणित से जानते हैं कि
\frac{1}{p^{2}}=\frac{1}{r^{2}}+\left(\frac{1}{r^{4}}\right)\left(\frac{d r}{d \theta}\right)^{2}
जहां P ध्रुव (मूलबिन्दु) O से P पर स्पर्शी रेखा पर लाम्बिक दूरी है
\Rightarrow \frac{1}{p^{2}}=u^{2}+\left(\frac{d u}{d \theta}\right)^{2} \cdots (7) \\ {\left[\therefore u=\frac{1}{r}, \frac{d u}{d \theta}=\left(-\frac{1}{r^{2}}\right)\left(\frac{d r}{d \theta}\right)\right]}
अब (7) के दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
-2\left(\frac{1}{p^{3}}\right)\left(\frac{d p}{d \theta}\right)=2 u\left(\frac{d u}{d \theta}\right)+2 \cdot\left(\frac{d u}{d \theta}\right)\left(\frac{d^{2} u}{d \theta^{2}}\right) \\ \Rightarrow-\left(\frac{1}{\rho^{3}}\right)\left(\frac{d p}{d \theta}\right)=\left[u+\left(\frac{d^{2} u}{d \theta^{2}}\right)\right] \frac{d u}{d \theta} \\ \Rightarrow-\left(\frac{1}{p^{3}}\right)\left(\frac{d p}{d r}\right)\left(\frac{d r}{d \theta}\right)=\left[u+\left( \frac{d^{2} u}{d \theta^{2}} \right)\right] \frac{d u}{d \theta} \\ \Rightarrow\left(\frac{1}{p^{3}}\right)\left(\frac{d p}{d r}\right)=u^{2}\left[u+ \left(\frac{d^{2} u}{d \theta^{2}}\right)\right] \\ \Rightarrow\left(\frac{1}{p^{3}}\right) \frac{d p}{d r}=\frac{P}{h^{2}} \\ \Rightarrow p=\frac{h^{2}}{p^{3}} \cdot \left(\frac{d p}{d r}\right)
यह सकेन्द्र कक्षा के अवकल समीकरण का पदिक रूप है।
सकेन्द्र कक्षा के किसी बिन्दु पर रैखिक वेग
(Linear velocity at any point of the central orbit).
प्रत्येक केन्द्रीय कक्षा में रैखिक वेग का परिमाण कण बिन्दु की स्पर्शरेखा पर केन्द्र से खींचे गए लम्ब की लम्बाई का व्युत्क्रमानुपाती है।
(In every central orbit the linear velocity varies inversely as the perpendicular from the centre upon the tangent to the path.):
सकेन्द्र कक्षा के किसी बिन्दु P पर कण के v वेग के अरीय तथा अनुप्रस्थ (radial and tranverse) घटक क्रमशः \dot{r} तथा r \dot{\theta} हैं इसलिए
v^{2} =(\dot{r})^{2}+(r \dot{\theta})^{2} \\ =\left[-h\left(\frac{d u}{d \theta}\right)^{2}+(h u)^{2}\right] [समीकरण (3) तथा (4) से]
अतः v^{2}=h^{2}\left[u^{2}+\left(\frac{d u}{d \theta}\right)^{2}\right]=\frac{h^{2}}{p^{2}} [समीकरण (7) से]
ध्रुव की ओर बल का नियम ज्ञात करना जिसके अधीन कोई कण वक्र r^{n}=a^{n} \cos n \theta को निर्मित करता है।
(To find the law of force towards the pole under which the curve r^{n}=a^{n} \cos n \theta can be described.)
यहां वक्र का समीकरण
r^{n}=a^{n} \cos n \theta \\ \Rightarrow u^{n} a^{n} \cos n \theta=1
दोनों पक्षों का लघुगुणक लेकर \theta के सापेक्ष अवकलन करने पर-
\frac{n}{u} \frac{d u}{d \theta}+\frac{1}{\cos n \theta}(-n \sin n \theta)=0 \\ \Rightarrow \frac{d u}{d \theta}=u \tan n \theta \cdots (2)
पुनः \theta के सापेक्ष अवकलन करने पर-
\frac{d^{2} u}{d \theta^{2}} =\frac{d u}{d \theta} \tan n \theta+u n \sec ^{2} n \theta \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}} =u\left(\tan ^{2} n \theta+n \sec ^{2} n \theta\right) [(2) से]
अब सकेन्द्र कक्षा के अवकल समीकरण से-
\Rightarrow \frac{P}{h^{2} u^{2}} =\frac{d^{2} u}{d \theta^{2}}+u \\ =u\left(\tan ^{2} n \theta+n \sec ^{2} n \theta+1\right) \\ =u(1+n) \sec ^{2} n \theta \\ =(n+1) a^{2 n} u^{2n+1} \\ \Rightarrow P =h^{2}(n+1) a^{2 n} u^{2n+3} \\ =\frac{h^{2}(n+1) a^{2 n}}{r^{2 n+3}} \\ \Rightarrow P \propto \frac{1}{r^{2 n+3}}
अतः केन्द्रीय बल P, बिन्दु की ध्रुवी दूरी के (2n+3) घातीय व्युत्क्रमानुपाती होगा।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Motion inside a smooth vertical circle
2.केन्द्रीय बल के अधीन गति के उदाहरण (Motion Under Central Force Examples)-
एक कण निम्न वक्र में केन्द्रीय बल P के अधीन चलता है, जहां बल केन्द्र ध्रुव है।प्रदर्शित कीजिए कि बल निम्न प्रकार है:
(A particle descibes the following curves under a central force P,when pole is the centre of force.Show that the force is as follows):
Example-1.r=a \sin n \theta ; p \propto \left(\frac{2 n^{2} a^{2}}{r^{5}}-\frac{n^{2}-1}{r^{3}}\right)
Solution–r=a \sin n \theta \\ \frac{1}{u}=a \sin n \theta \\ \Rightarrow 1=a u \sin n \theta
दोनों पक्षों का लघुगुणक लेने पर-
\log 1 =\log a+\log u+\log (\sin \theta) \\ \Rightarrow 0 =\log a+\log u+\log (\sin n \theta)
दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
0=0+\frac{1}{u} \cdot \frac{d u}{d \theta}+\frac{n \cos n \theta}{\sin n \theta} \\ \Rightarrow \frac{d u}{d \theta}=-\frac{n u \cos n \theta}{\sin n \theta} \cdots(1)
पुनः दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\frac{d^{2} u}{d \theta^{2}}=-n\left[ \frac{\sin n \theta \left(\frac{d u }{d \theta} \cos n \theta-n u \sin n \theta \right)-u \cdot \cos n \theta \cdot n \cos n \theta}{ \sin ^{2} n \theta}\right] \\ = \frac{-n\left[\sin n \theta\left(-\frac{n u \cos n \theta}{\sin n \theta} \cdot \cos n \theta-n u \sin n \theta\right) -nu \cos ^{2} n \theta\right]}{\sin ^{2} n \theta} \\ =n^{2} u\left[\frac{\cos ^{2} n \theta +\sin ^{2} n \theta+\cos ^{2} n \theta}{\sin ^{2} n \theta}\right] \\ \Rightarrow \frac{d^{2} u} {d \theta^{2}} =n^{2} u\left[\frac{\cos ^{2} n \theta +1}{\sin ^{2} n \theta}\right] \cdots(2)
ध्रुव की ओर बल के अधीन सकेन्द्र कक्षा का अवकल समीकरण
\frac{P}{h^{2} u^{2}} =\frac{d^{2} u}{d \theta^{2}}+u \\ =n^{2} u\left[\frac{\cos ^{2} n \theta +1}{\sin ^{2} n \theta}\right]+u
=n^{2} u\left[\frac{\left(1-\sin ^{2} n \theta\right)+1}{\sin ^{2} n \theta }\right]+u \\ =u\left[\frac{n^{2}\left(1-\sin ^{2} n \theta\right)}{\sin ^{2} n \theta }+\frac{n^{2}}{\sin ^{2} n \theta}+1\right] \\ \Rightarrow P =h^{2} u^{3}\left[ \frac{n^{2}} {\sin ^{2} n \theta}-n^{2} +\frac{n^{2}}{\sin^{2} n \theta}+1\right] \\ =h^{2} u^{3}\left[n^{2} a^{2} u^{2}-n^{2}+n^{2} a^{2} u^{2}+1\right] \\ =h^{3}\left[n^{2} a^{2} u^{5}-n^{2} u^{3}+n^{2} a^{2} u^{5}+u^{3}\right] \\ \Rightarrow P=h^{3}\left[2 n^{2} a^{2} u^{5}-\left(n^{2}-1\right) u^{3}\right] \\ =h^{3}\left[\frac{2 n^{2} a^{2}}{r^{5}}-\frac{n^{2}-1}{r^{3}}\right]\left[u=\frac{1}{r}\right] \\ \Rightarrow P \propto \left(\frac{2 n^{2} a^{2}}{r^{5}}-\frac{n^{2}-1}{r^{3}}\right)
उपर्युक्त उदाहरण के द्वारा केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को समझ सकते हैं।
Example-2.r=a \cos n \theta ; P \propto \left(\frac{2 n^{2} a^{2}}{r^{5}}-\frac{n^{2}-1}{r^{3}}\right)
Solution–r=a \cos n \theta \\ \frac{1}{u}=a \cos n \theta \quad\left[r=\frac{1}{a}\right] \\ \Rightarrow 1=au \cos n \theta
दोनों पक्षों का लघुगुणक लेने पर-
\log 1=\log a+\log u+\log \cos n \theta \\ \theta=\log a+\log u+\log \cos n \theta
दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
0=0+\frac{1}{u} \frac{d u}{d \theta}-\frac{n \sin n \theta}{\cos n \theta} \\ \Rightarrow \frac{d u}{d \theta}=un \frac{\sin n \theta}{\cos n \theta} \cdots(1)
पुनः दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\Rightarrow \frac{d^{2} u}{d \theta^{2}}=n\left[\frac{\cos n \theta (\sin n \theta \frac{du}{d \theta}+ nu \cos n \theta) + u \sin n \theta \cdot n \sin n \theta}{\cos ^{2} n \theta}\right] \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=n \frac{[\cos n \theta\left(\frac{u n \sin n \theta}{\cos n \theta} \sin n \theta+n u \cos n \theta\right)+un \sin^{2} n \theta]}{\cos ^{2} n \theta} \\ \frac{d u}{d \theta^{2}}=n^{2} u \frac{\left[\sin ^{2} n \theta+\cos ^{2} n \theta+\sin ^{2} n \theta\right]}{\cos ^{2} n \theta} \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=n^{2} u\left(\frac{\sin ^{2} n \theta+1}{\cos ^{2} n \theta}\right) \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=n^{2} u\left(\frac{1-\cos ^{2} n \theta+1}{\cos ^{2} n \theta}\right) \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=n^{2} u\left(\frac{2-\cos ^{2} n \theta}{\cos ^{2} n \theta}\right) \cdots(2)
ध्रुव की ओर बल के अधीन सकेन्द्र कक्षा का अवकल समीकरण
\frac{P}{h^{2} u^{2}} =\frac{d^{2} u}{d \theta^{2}}+u \\=n^{2} u\left(\frac{2-\cos ^{2} n \theta}{\cos ^{2} n \theta}\right)+u \\ =u\left[\frac{2 n^{2}}{\cos ^{2} n \theta}-n^{2}+1\right] \\ \Rightarrow P=h^{2} u^{3}\left[2 n^{2} \cdot a^{2} u^{2}-n^{2}+1\right] \\ \Rightarrow P=h^{2}\left[2 n^{2} a^{2} u^{5}-\left(n^{2}-1\right) u^{3}\right] \\ \Rightarrow P=h^{2}\left(\frac{2 n^{2} a^{2}}{r^{5}}-\frac{n^{2}-1}{r^{3}}\right)\left[\because u=\frac{1}{r}\right] \\ \Rightarrow P \propto \frac{2 n^{2} a^{2}}{r^{5}}-\frac{n^{2}-1}{r^{3}}
उपर्युक्त उदाहरण के द्वारा केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को समझ सकते हैं।
Example-3.r^{n} \cos n \theta =a^{n} ; P \propto r^{2 n-3}
Solution–r^{n} \cos n \theta =a^{n} \\ \frac{1}{u^{n}} \cos n \theta=a^{n} \quad\left[r=\frac{1}{u}\right] \\ \Rightarrow a^{n} u^{n}=\cos n \theta
दोनों पक्षों का लघुगुणक लेने पर-
\Rightarrow n \log a+n \log u=\log (\cos n \theta)
दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
0+n \cdot \frac{1}{u} \frac{d u}{d \theta}=-\frac{n \sin n \theta}{\cos n \theta} \\ \frac{d u}{d \theta}=-u \frac{\sin n \theta}{\cos n \theta} \cdots(1)
पुनः दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\frac{d^{2} u}{d \theta^{2}}=-\left[\frac{\cos n \theta\left(\sin n \theta \cdot \frac{d u}{d \theta}+u \cdot n \cos n \theta\right)+u \sin n \theta \cdot n \sin n \theta}{\cos ^{2} n \theta}\right] \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}} =-\left[\frac{\cos n \theta\left(\sin n \theta \cdot\left(-\frac{u \sin n \theta}{\cos n \theta}\right)+n\cos n \theta \right)+n u \sin ^{2} n \theta}{\cos ^{2} n \theta}\right]\\ =u\left[\frac{\sin ^{2} n \theta-n \cos ^{2} n \theta-n \sin ^{2} n \theta}{\cos ^{2} n \theta}\right] \\ =u\left[\frac{\sin ^{2} n \theta-n}{\cos ^{2} n \theta}\right] \\ =u\left(\frac{1-\cos ^{2} n \theta-n}{\cos ^{2} n \theta}\right) \\ \frac{d^{2} u}{d \theta^{2}}= \frac{u\left(1-\cos ^{2} n \theta-n\right)}{\cos ^{2} n \theta} \cdots (2)
ध्रुव की ओर बल के अधीन सकेन्द्र कक्षा का अवकल समीकरण
\frac{P}{h^{2} u^{2}}=\frac{d^{2} u}{d \theta^{2}}+u \\ = \frac{u\left(1-\cos ^{2} n \theta-n\right)}{\cos ^{2} n \theta}+u \\ P=h^{2} u^{3}\left[\frac{1-\cos ^{2} n \theta-n}{\cos ^{2} n \theta}+1\right] \\ \Rightarrow P=h^{2} u^{3}\left[\frac{1-\cos ^{2} n \theta-n+\cos ^{2} n \theta}{\cos ^{2} n \theta}\right] \\ \Rightarrow P=\frac{h^{2} u^{3}(1-n)}{\cos ^{2} n \theta} \\ \Rightarrow P=\frac{h^{2}(1-n)}{r^{3}\left(\frac{a^{2} n}{r^{2}n}\right)}
[\because u=\frac{1}{r} तथा \cos n \theta=\frac{a^{n}}{r^{n}}]
\Rightarrow P=\frac{r^{2 n-3} h^{2}(1-n)}{a^{2 n}} \\ \Rightarrow P \propto r^{2 n-3}
उपर्युक्त उदाहरण के द्वारा केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को समझ सकते हैं।
Example-4.वृत्त,जिसकी परिधि पर ध्रुव है;
(Circle,pole on the Circumference)
P \propto \frac{1}{r^{5}}
Solution-r =a \cos \theta \\ \frac{1}{u} =a \cos \theta \quad\left[r=\frac{1}{u}\right] \\ \Rightarrow 1 =au \cos \theta
दोनों पक्षों का लघुगुणक लेने पर-
\Rightarrow \log 1 =\log a+\log u+\log \cos \theta \\ \Rightarrow 0 =\log a+\log u+\log \cos \theta
दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\Rightarrow 0=\frac{1}{u} \frac{d u}{d \theta}-\frac{\sin \theta}{\cos \theta} \\ \Rightarrow \frac{d u}{d \theta}=\frac{u \sin \theta}{\cos \theta} \cdots(1)
पुनः दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\frac{d^{2} u}{d \theta^{2}}=\frac{\cos \theta\left(\frac{d u}{d \theta} \sin \theta+u \cos \theta\right)+u \sin \theta \sin \theta}{\cos ^{2} \theta} \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=\frac{\cos \theta\left(\frac{u \sin \theta}{\cos \theta} \sin \theta+u \cos \theta\right)+u \sin ^{2} \theta}{\cos ^{2} \theta} [(1) से]
\Rightarrow \frac{d^{2} u}{d \theta^{2}}= \frac{u\left[\sin ^{2} \theta+\cos ^{2} \theta+\sin ^{2} \theta\right]}{\cos ^{2} \theta} \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=u \frac{\left(1+\sin ^{2} \theta\right)}{\cos ^{2} \theta} \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=u \frac{\left(1+1-\cos ^{2} \theta\right)}{\cos ^{2} \theta} \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=\frac{u \left(2-\cos ^{2} \theta\right)}{\cos ^{2} \theta} \cdots(2)
ध्रुव की ओर बल के अधीन सकेन्द्र कक्षा का अवकल समीकरण
\frac{P^{2}}{h^{2} u^{2}} =\frac{d^{2} u}{d \theta^{2}}+u \\ =\frac{u\left(2-\cos ^{2} \theta\right)}{\cos ^{2} \theta}+u [(2) से]
=u\left[\frac{2-\cos ^{2} \theta}{\cos ^{2} \theta}+1\right] \\ =u \left[\frac{2-\cos ^{2} \theta+\cos ^{2} \theta}{\cos ^{2} \theta}\right] \\ =\frac{2 u}{\cos ^{2} \theta} \\ \Rightarrow P^{2} =\frac{2 h^{2} u^{3}}{\cos ^{2} \theta} \\ =\frac{2 h^{2}}{r^{3}\left(\frac{r^{2}}{a^{2}}\right)}
[\because u=\frac{1}{r} तथा \cos \theta=\frac{r}{a}]
P^{2}=\frac{2 h^{2} a^{2}}{r^{5}} \\ \Rightarrow p^{2} \propto \frac{1}{r^{5}}
उपर्युक्त उदाहरण के द्वारा केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को समझ सकते हैं।
Example-5.a u=\tanh \left(\frac{\theta}{\sqrt{2}}\right) ; P \propto \frac{1}{r^{5}}
Solution-a u=\tanh \left(\frac{\theta}{\sqrt{2}}\right)
दोनों पक्षों का लघुगुणक लेने पर-
\log a+\log u=\log \left(\tanh \left(\frac{\theta}{\sqrt{2}}\right)\right)
दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\frac{1}{u} \frac{d u}{d \theta}=\frac{\operatorname{sech}^{2}\left(\frac{\theta}{\sqrt{2}}\right) \cdot \frac{1}{\sqrt{2}}}{\tanh \left(\frac{\theta}{\sqrt{2}}\right)} \\ \Rightarrow \frac{d u}{d \theta}=\frac{u}{\sqrt{2}} \cdot \frac{\operatorname{sech} ^{2} \left(\frac{\theta}{\sqrt{2}}\right)}{\tanh \left(\frac{\theta}{\sqrt{2}}\right)} \cdots (1)
पुनः दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\frac{d^{2} u}{d \theta^{2}}= \frac{\begin{pmatrix}\frac{1}{\sqrt{2}} [\tanh \left(\frac{\theta}{\sqrt{2}} \right)\left(\frac{d u}{d \theta} \cdot \operatorname{sech}^{2}\left(\frac{\theta}{\sqrt{2}}\right)-\frac{u \cdot 2}{\sqrt{2}} \operatorname{sech}^{2} \left(\frac{\theta}{\sqrt{2}}\right) \tanh \left(\frac{\theta}{\sqrt{2}}\right) \right) \\ -\frac{1}{\sqrt{2}} u \operatorname{sech}^{2} \left(\frac {\theta}{\sqrt{2}}\right) \cdot \operatorname{sech}^{2}\left(\frac{\theta}{\sqrt{2}}\right)] \end{pmatrix}}{ \tanh^{2} \left(\frac{\theta}{\sqrt{2}}\right)} \\ \frac{d^{2} u}{d \theta^{2}}=\frac{ \begin{pmatrix} \frac{1}{\sqrt{2}} [\tanh ( \frac { \theta } {\sqrt{2}} ) ( \frac{u}{\sqrt{2}} \frac{ \operatorname{sech}^{2} \left(\frac{a}{\sqrt{2}}\right)}{\tanh \left(\frac{\theta}{\sqrt{2}}\right)} \cdot \operatorname{sech}^{2} \left(\frac{\theta}{\sqrt{2}}\right) \\ -\sqrt{2} u \operatorname{sech}^{2} \left(\frac{\theta}{\sqrt{2}} \right) \tanh ( \frac { \theta } {\sqrt{2}})) -\frac{u}{\sqrt{2}} \operatorname{sech}^{4} \left(\frac{\theta}{\sqrt{2}}\right)] \end{pmatrix}}{\tanh ^{2} \frac{\theta}{\sqrt{2}}} \\ =\frac{u}{2}\left[\frac {\operatorname{sech}^{4}\left(\frac{\theta}{\sqrt{2}} \right) -2 \operatorname{sech}^{2} \left(\frac {\theta}{\sqrt{2}}\right) \tanh ^{2}\left(\frac{\theta}{\sqrt{2}}\right)-\operatorname{sech}^{4} \left (\frac{\theta}{\sqrt{2}}\right)}{\tanh ^{2}\left(\frac{\theta}{\sqrt{2}}\right)}\right] \\ \Rightarrow \frac{d^{2} u}{d \theta^{2}}=-u \operatorname{sech}^{2} \left(\frac{\theta}{\sqrt{2}}\right) \cdots(2)
ध्रुव की ओर बल के अधीन सकेन्द्र कक्षा का अवकल समीकरण
\frac{P^{2}}{h^{2} u^{2}}=\frac{d^{2} u}{d \theta^{2}}+u \\ \frac{P^{2}}{h^{2} u^{2}} =-u \operatorname{sech}^{2}\left(\frac{\theta}{\sqrt{2}}\right)+u[(2) से]
=u\left[1-\operatorname{sech}^{2}\left(\frac{\theta}{\sqrt{2}}\right)\right] \\ =u \cdot \tanh ^{2}\left(\frac{\theta}{\sqrt{2}}\right) \\ P=h^{2} u^{3} \tanh ^{2}\left(\frac{\theta}{\sqrt{2}}\right) \\ \Rightarrow P =h^{2} u^{3} a^{2} u^{2} \\ \Rightarrow P =h^{2} a^{2} u^{5} \\ \Rightarrow P=\frac{h^{2} a^{2}}{r^{5}}\left[\because u=\frac{1}{r}\right] \\ \Rightarrow P \propto \frac{1}{r^{5}}
उपर्युक्त उदाहरण के द्वारा केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को समझ सकते हैं।
Example-6. \frac{l}{r}=1+e \cos \theta ; P \propto \frac{1}{r^{2}}
Solution-\frac{l}{r}=1+e \cos \theta \\ \Rightarrow u l=1+e \cos \theta \left[\because \frac{1}{r}=u\right] \\ u=\frac{1}{l}+\frac{e}{l} \cos \theta
दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\frac{d u}{d \theta}=-\frac{e}{l} \sin \theta \cdots(1)
पुनः दोनों पक्षों का \theta के सापेक्ष अवकलन करने पर-
\frac{d^{2} u}{d \theta^{2}}=-\frac{e}{l} \cos \theta \cdots (2)
ध्रुव की ओर बल के अधीन सकेन्द्र कक्षा का अवकल समीकरण
\frac{P^{2}}{h^{2} u^{2}}=\frac{d^{2} u}{d \theta^{2}}+u \\ \Rightarrow \frac{P^{2}}{h^{2} u^{2}}=-\frac{e}{l} \cos \theta+u [(2) से]
\Rightarrow \frac{P^{2}}{h^{2} u^{2}}=-\frac{e}{l} \cos \theta+\frac{1}{l}+\frac{e}{l} \cos \theta \\ \Rightarrow \frac{P^{2}}{h^{2} u^{2}}=\frac{1}{l} \\ \Rightarrow P^{2}=\frac{h^{2} u^{2}}{l} \\ \Rightarrow P^{2}=\frac{h^{2}}{l r^{2}} \left[u=\frac{1}{r}\right] \\ \Rightarrow P^{2} \propto \frac{1}{r^{2}}
उपर्युक्त उदाहरणों के द्वारा केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को समझ सकते हैं।
3.केन्द्रीय बल के अधीन गति की समस्याएं (Motion Under Central Force Problems),केन्द्रीय बल के अधीन गति की समस्याएं एवं हल (Central Force Problems and Solutions)-
ध्रुव बिन्दु की ओर बल का नियम ज्ञात करिए जिसके अधीन कोई कण वक्र
(Find the law force towards the pole under which the curve)
(1.) r=a e^{\theta \cot \alpha} (समानकोणिक सर्पिल है)[Equiangular spiral]
(2.)r=a \tan \theta गतिमान है (is described)
(3.)ध्रुव बिन्दु की ओर बल P के अधीन एक कण \left(\frac{a}{r}\right)=e^{n \theta}, n \theta, \operatorname{coshn} \theta या \sinh n \theta निर्मित करता है तो बल का नियम ज्ञात कीजिए।
(A particle descibes the following curves under a force P to the pole.Find the law of force \left(\frac{a}{r}\right)=e^{n \theta}, n \theta, \operatorname{coshn} \theta or \sinh n \theta )
(4.)एक कण निम्न वक्र में केन्द्रीय बल P के अधीन चलता है, जहां बल केन्द्र ध्रुव है।प्रदर्शित कीजिए कि बल निम्न प्रकार है:
(A particle descibes the following curves under a central force P,when pole is the centre of force.Show that the force is as follows): r=a \frac{\cosh \theta-1}{\cosh \theta+2} ; P \propto \cdot \frac{1}{r^{4}}
उत्तर (Answers): (1) P \propto \frac{1}{r^{3}} \\ (2)P=\frac{h^{2}}{r^{3}}\left(3+\frac{2 a^{2}}{r^{2}}\right) \\ (3)P \propto \frac{1}{r^{3}}
उपर्युक्त सवालों को हल करने पर केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को ठीक से समझा जा सकता है।
Also Read This Article:-Motion Outside Soomth Vertical Circle
4.केन्द्रीय बल के अधीन गति (Motion Under Central Force) के बारे में अक्सर पूछे जाने वाले प्रश्न-
प्रश्न:1.आप केंद्रीय बल की गणना कैसे करते हैं?(How do you calculate central force?)
उत्तर-इसके विपरीत,यदि गति के अधीन एक संरक्षी बल F प्लानर (समतलीय) है और त्रिज्या r और वेग v की सभी प्रारंभिक स्थितियों के लिए अचर अनुप्रस्थ वेग है,तो अज़ीमुथल त्वरण aφ हमेशा शून्य है।इसलिए, न्यूटन के दूसरे नियम, F =ma द्वारा,बल एक केंद्रीय बल है।
इस केन्द्रीय बल को ध्रुव की ओर बल के अधीन सकेन्द्र कक्षा का अवकल समीकरण की सहायता से ज्ञात करते हैं।
प्रश्न:2.कौनसा केंद्रीय बल को हल करने के लिए सही समीकरण है ? (Which is the correct equation for solving central force?)
उत्तर-केंद्रीय बल मुख्य रूप से उन वस्तुओं द्वारा अनुभव किया जाता है जो एक समान वृत्तीय गति में होते हैं क्योंकि बल एक निश्चित बिंदु पर वस्तु को रखता है।
इसे निम्न अवकल समीकरण के द्वारा ज्ञात किया जाता है-
\Rightarrow \frac{P}{h^{2} u^{2}} =\frac{d^{2} u}{d \theta^{2}}+u
प्रश्न:3.केंद्रीय बल गति क्या है? (What is central force motion?)
उत्तर-किसी भी बल को एक केंद्रीय बल कहा जाता है जब इसे हमेशा एक निश्चित बिंदु की ओर निर्देशित किया जाता है, और इसका परिमाण एक निश्चित बिंदु (O) से कण की दूरी r पर निर्भर होती है।एक कण की केंद्रीय बल गति की प्रासंगिकता: कई प्राकृतिक घटनाएं भौतिक विज्ञान में केंद्रीय बल को परिभाषित करती हैं।
प्रश्न:4.क्या केंद्रीय बल उस बिंदु के बारे में टाॅर्क्स को जन्म दे सकता है? (Can a central force give rise to torque about that point?)
उत्तर-केंद्रीय बल उन वस्तुओं पर टॉर्क्स (torques) (केंद्रीय बिंदु के सापेक्ष) नहीं डालते हैं जो वे प्रभावित करते हैं, और इसलिए केंद्रीय संदर्भ बिंदु के चारों ओर कोणीय गति को संरक्षित किया जाता है।
प्रश्न:5.एक केंद्रीय बल क्षेत्र में अरीय वेग है (In a central force field the areal velocity is)
उत्तर-h का परिमाण भी अरीय वेग के दुगुने के बराबर होता है, जो कि केंद्र के सापेक्ष कण द्वारा जिस क्षेत्र में बह रहा है। इस प्रकार, अरीय वेग किसी भी प्रकार के केंद्रीय बल द्वारा कार्य किए गए एक कण के लिए स्थिर होता है;यह केप्लर का दूसरा नियम है।जहां h=r^2(\frac{d \theta}{dt})=अचर
उपर्युक्त प्रश्नों के उत्तर द्वारा केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को समझ सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा केन्द्रीय बल के अधीन गति (Motion Under Central Force),ध्रुव बिन्दु की ओर बल का नियम ज्ञात करो (Find Law of Force Towards Pole) को समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |