1.समतल ज्यामिति परिचय एवं रेखाएं तथा कोण (Plane Geometry and Line and Angle)-

समतल ज्यामिति परिचय एवं रेखाएं तथा कोण (Plane Geometry and Line and Angle) की नींव भारत में प्राचीन काल में ही पड़ गई थी।हड़प्पा और मोहनजोदड़ो (दोनों अब पाकिस्तान में),कालीबंगा (राजस्थान) एवं लोथल (गुजरात) में खुदाइयों से प्राप्त अवशेषों के आधार पर यह स्पष्ट रूप से प्रमाणित होता है कि प्राचीन भारत में ढाई सौ ईसा पूर्व से 1750 ईसा पूर्व की काल अवधि में एक बड़े क्षेत्र में विकसित सभ्यता फली फूली।इस सभ्यता के अवशेषों से यह भी प्रमाणित होता है कि यहां के निवासियों को ज्यामिति एवं ज्यामितीय रचनाओं का विशेष ज्ञान था। इसी ज्ञान के आधार पर उन्होंने भवनों,सड़कों वृत्तों,अर्द्धगोलों का निर्माण किया था जिसमें क्षेत्रमिति का विशेष महत्त्व होता है।
रेखागणित एवं ज्यामिति की जन्मस्थली भी भारत रहा है। 1000 ईसा पूर्व से 500 ईसा पूर्व के शुल्व काल या वेदांग-ज्योतिषकाल में ही रेखागणित तथा ज्यामिति की नींव पड़ गई थी।इस काल में इसे विभिन्न नामों से जाना जाता था जैसे शुल्व गणित,शुल्व विज्ञान,शुल्व गणित,रज्जु संख्यान्।शुल्व का पर्यायवाची रज्जु होने के कारण इसे रज्जु गणित भी कहा गया जो आगे चलकर “रेखागणित” में परिणित हो गया।
प्राचीनकाल से यज्ञों के लिए वेदियां बनाई जाती थी,उनका आधार भी ज्यामिति ही रहता था।यज्ञों के अनुसार भिन्न-भिन्न आकार प्रकार की वेदियां बनाने की आवश्यकता पड़ी जिसके लिए विभिन्न प्रकार की आकृतियों जैसे वर्गाकार,अर्द्धवृत्ताकार,आयताकार,त्रिभुजाकार इत्यादि का विकास हुआ।वेदियों की रचना में इस बात का भी ध्यान रखना आवश्यक था कि सभी वेदियों का क्षेत्रफल मानक वेदी के बराबर हो।अतः इसके लिए ज्यामितीय रचनाओं का ज्ञान अत्यंत आवश्यक था जैसे सरल रेखा पर वर्ग बनाना,वर्ग को बराबर क्षेत्रफल वाले वृत्त में परिवर्तित करना,वर्ग के परिगत वृत्त खींचना एवं वर्ग के अंतर्गत वृत्त खींचना,वृत्त के क्षेत्र को द्विगुणित करना इत्यादि।
(1.)ज्यामिति की आधारभूत संकल्पनाएं (Basic Geometry Concepts)-
कुछ मूलभूत संकल्पनाओं को आधार बनाकर ज्यामिति का अध्ययन किया जाता है।इन आधारभूत संकल्पनाओं को अनुभवों और उदाहरणों द्वारा ही समझा जाता है,इनके लिए किसी भी प्रकार की उपपत्तियां (Proofs) नहीं दी जाती है।ज्यामिति के अध्ययन में तीन आधारभूत संकल्पनाएं मानी जाती है।(1.)बिन्दु (2.)रेखा (3.)समतल।जिन्हें कुछ उदाहरणों की सहायता से समझने का प्रयास करेंगे।
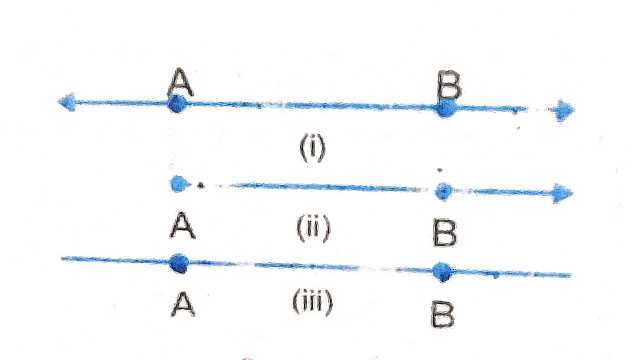
(1.)बिन्दु (Point)-अत्यंत तेज नोकवाली बारीक पेंसिल द्वारा लगाया गया एक चिन्ह बिंदु का उदाहरण है। साधारणतः बिन्दु को अंग्रेजी वर्णमाला के बड़े अक्षरों अर्थात् A,B,C,D इत्यादि द्वारा दर्शाते हैं।
(2.)रेखा (Line)- सरल रेखा दो बिंदुओं को उनके मध्य स्थित सभी बिंदुओं को परस्पर सीधा मिलाते हुए खींची हुई दोनों तरफ अनन्त की ओर अग्रसर होती है।यदि इन बिन्दुओं में से एक को स्थिर करते हुए दूसरे को अनंत की ओर ले जाया जाए तो यह एक किरण को निरूपित करेगी एवं यदि दोनों बिन्दुओं को स्थिर कर दिया जाए तो बनने वाली आकृति को रेखाखंड कह सकते हैं।निम्न चित्र में क्रमशः रेखा \underset{AB}{\leftrightarrow },किरण \underset{AB}{\rightarrow} ,रेखाखंड AB कहते हैं।

(3.)समतल (Plane)-वह जिस पर स्थित किन्हीं दो बिन्दुओं को परस्पर मिलाते हुए एक सरल रेखा खींचने पर उनके मध्य स्थित सभी बिंदु उस पृष्ठ पर स्थित हो तो ऐसे पृष्ठ को समतल कहते हैं।
ज्यामिति का अध्ययन करने के लिए कुछ अभिगृहीत (वे रचनाएं जिन्हें बिना प्रमाण सत्य माना जाता है तथा इनके आधार पर अन्य ज्यामितीय रचनाओं को सिद्ध किया जाता है) आवश्यक है जो मुख्यतः निम्न हैं-
(1.)एक रेखा पर अनंत बिंदु होते हैं।
(2.)एक रेखाखंड को अपनी इच्छानुसार कितनी ही लंबाई तक बढ़ाया जा सकता है।
(3.)एक बिंदु से अनंत रेखाएं खींची जा सकती है।
(4.)दो बिंदुओं से गुजरती हुई एक और केवल एक ही सरल रेखा खींची जा सकती है।
(5.)एक दी गई रेखा के समांतर किसी बाह्य बिंदु से एक और केवल एक ही रेखा खींची जा सकती है।
(6.)सभी समकोण समान होते हैं।
(7.)समान पूरक और संपूरक कोण क्रमशः आपस में समान होते हैं।
(8.)एक ही रेखाखंड को केवल एक ही बिंदु पर समद्विभाजित किया जा सकता है।
(9.)एक कोण को केवल एक ही रेखा द्वारा विभाजित किया जा सकता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Properties of Parallelogram

2.समतल ज्यामिति परिचय एवं रेखाएं तथा कोण के उदाहरण (Plane Geometry and Line and Angle Examples)-

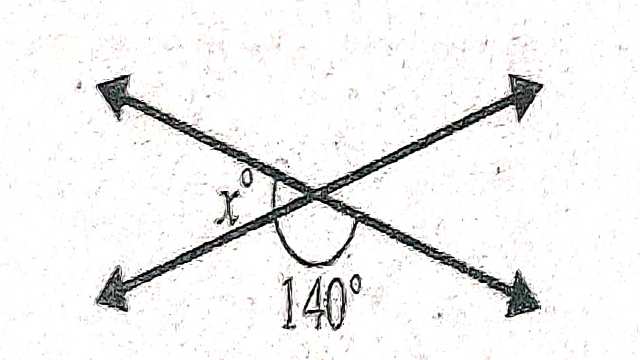
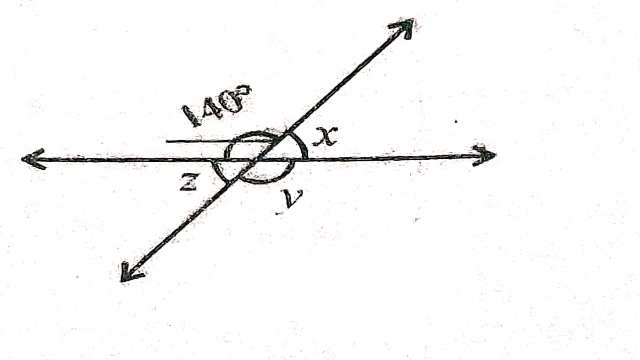
Example-1.चित्र से \angle x का मान बताइए।

Solution–\angle x+140^{\circ}=180^{\circ} (रैखिक कोण युग्म)

\angle x=180^{\circ}-140^{\circ} \\ \angle x=40^{\circ}
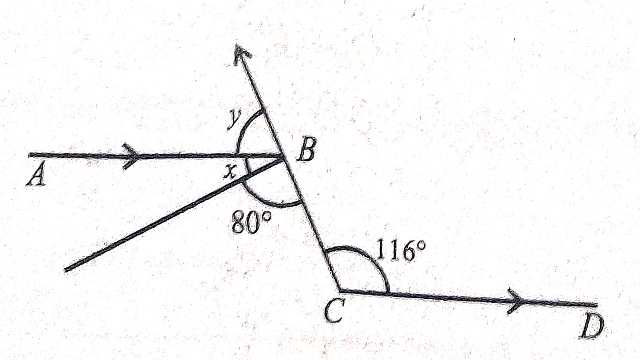
Example-2.दिए गए चित्र में रेखाएं AB \parallel CD है।चित्र में दिए गए कोणों से \angle x तथा \angle y ज्ञात कीजिए।

Solution–AB \parallel CD \\ \angle ABC= \angle BCD(एकान्तर कोण)
\Rightarrow \angle x+80^{\circ}=116^{\circ} \\ \Rightarrow \angle x=116^{\circ}-80^{\circ} \\ \Rightarrow \angle x=36^{\circ} \\ \angle y+\angle A B C=180^{\circ} (रैखिक कोण युग्म)

\Rightarrow \angle y+116^{\circ}=180^{\circ} \\ \Rightarrow \angle y=180^{\circ}-116^{\circ} \\ \Rightarrow \angle y=64^{\circ}, \quad \angle x=36^{\circ}
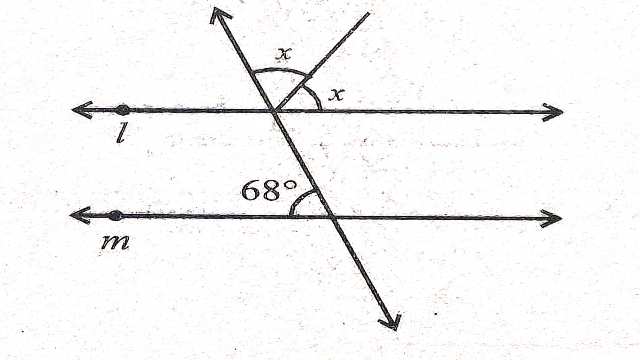
Example-3.चित्र में रेखाएं l तथा m समान्तर हैं तो \angle x का मान ज्ञात कीजिए। कारण भी स्पष्ट कीजिए।

Solution–l \parallel m  \\ \angle x+\angle x+68^{\circ}=180^{\circ}  (रैखिक कोण युग्म)

\Rightarrow 2 \angle x=180^{\circ}-68^{\circ} \\ \Rightarrow 2 \angle x=112^{\circ} \\ \Rightarrow \angle x=\frac{112^{\circ}}{2} \\ \Rightarrow \angle x=56^{\circ}
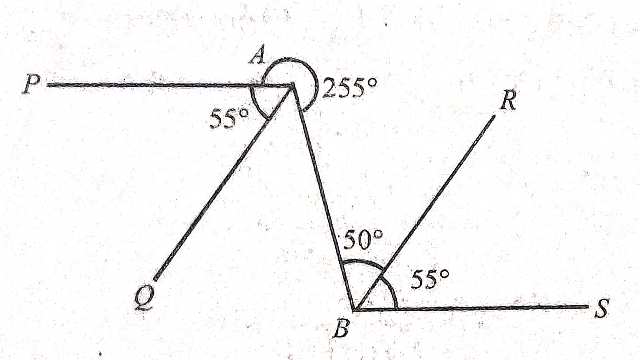
Example-4.चित्र में कौन-कौनसी रेखाएं समान्तर हैं और क्यों?

Solution–\angle B A Q+\angle P A Q+\angle B A P=360^{\circ} (एक बिन्दु पर बननेवाले कोण)

\angle B A Q+55^{\circ}+255^{\circ}=360^{\circ} \\ \Rightarrow \angle B A Q+310^{\circ}=360^{\circ} \\ \Rightarrow \angle B A Q=360^{\circ}-310^{\circ} \\ \Rightarrow \angle B A Q=50^{\circ} \\ \therefore B A Q=\angle A B R
ये एकान्तर कोण हैं तथा बराबर हैं अतः

A Q \| B R \\ \angle B A P =\angle B A Q+\angle P A Q \\ =50^{\circ}+55^{\circ} \\ \Rightarrow \angle B A P=105^{\circ} \\ \Rightarrow \angle B A P=\angle A B S
ये एकान्तर कोण हैं तथा बराबर हैं अतः

AP \parallel BS
अतः AQ \parallel BR तथा AP \parallel BS
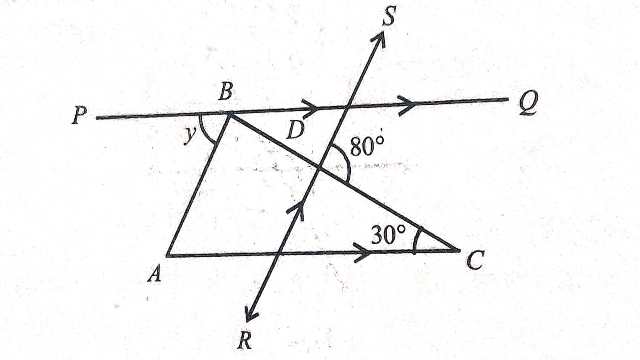
Example-5.सामने दिए गए चित्र में AC \parallel PQ एवं AB \parallel RS तो \angle y का मान ज्ञात कीजिए।प्रयोग में आनेवाले कथनों के कारण भी लिखिए।

Solution–\angle B D R=\angle S D C(शीर्षाभिमुख कोण)

\angle B D R=80^{\circ} \\ AB \parallel RS एवं BC तिर्यक रेखा काटती हैं अतः
\angle A B C+\angle B D R=180^{\circ} (अन्त: कोणों का योग)

\Rightarrow \angle A B C+80^{\circ}=180^{\circ} \\ \Rightarrow \angle A B C=180^{\circ}-80^{\circ} \\ \Rightarrow A B C=100^{\circ}
\triangle ABC में

\angle B A C+\angle A B C+\angle A C B=180^{\circ} \\ \Rightarrow \angle BAC+100^{\circ}+30^{\circ}= 180^{\circ} \\ \Rightarrow \angle B A C+130^{\circ}=180^{\circ} \\ \Rightarrow \angle B A C=180^{\circ}- 130^{\circ} \\ \Rightarrow \angle B A C=50^{\circ} \\ A C \parallel P Q
अतः \angle P B A=\angle B A C (एकान्तर कोण)

\angle y=50^{\circ}
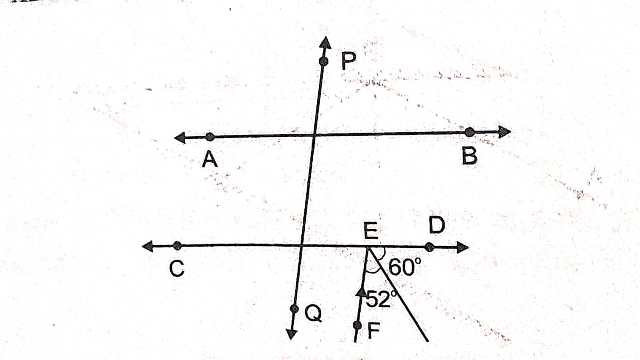
Example-6.चित्र में AB \parallel CD एवं P Q \parallel EF हो तो \angle x का मान ज्ञात कीजिए।

Solution–P Q \parallel EF \\ \angle X=\angle D E F (संगत कोण)

\angle x= 60^{\circ}+52^{\circ} \\ \angle x=112^{\circ}
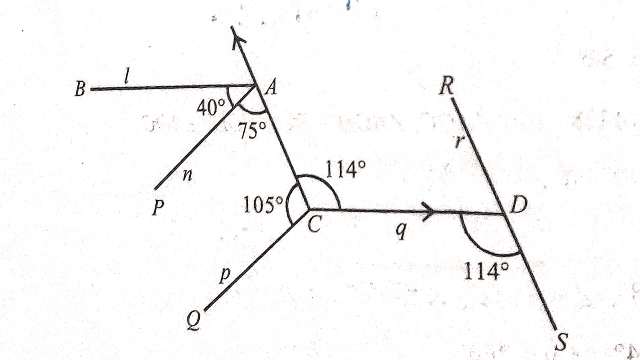
Example-7.चित्र में रेखाओं l,m,n,p,q एवं r में से कौन-कौनसी रेखाएं समान्तर हैं? और क्यों?

Solution–\angle PA C+\angle A C Q =75^{\circ}+105^{\circ} \\ \Rightarrow \angle P A C+\angle A C Q=180^{\circ}
अन्त: कोणों का योग 180° है अतः

n \parallel p \\  \angle ACD=\angle CDS
ये एकान्तर कोण हैं तथा बराबर हैं अतः

m \parallel r
m अर्थात् AC रेखा है।
अतः n \parallel p तथा m \parallel r
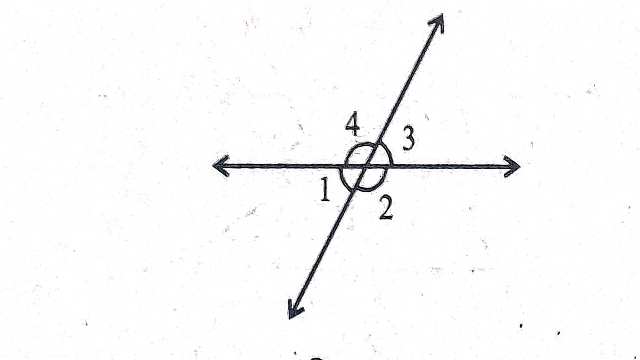
Example-8.चित्र में दो सरल रेखाएं एक-दूसरे को प्रतिच्छेद कर रही है।अंकित कोणों में यदि \angle 1+\angle 2+\angle 3=230^{\circ}  हो तो \angle 1 एवं \angle 4 ज्ञात कीजिए।

Solution–\angle 1+\angle 2+\angle 3+\angle 4=360^{\circ}
(एक बिन्दु पर बने कोणों का योग)

\Rightarrow \quad 230^{\circ}+\angle 4=360^{\circ}  \\ \left(\angle 1+\angle 2+\angle 3=230^{\circ}\right) \\ \Rightarrow \quad \angle 4=360^{\circ}-230^{\circ} \\ \Rightarrow \angle 4=130^{\circ} \\ \angle 1+\angle 4=180^{\circ} (रेखिक कोण युग्म)

\Rightarrow \angle 1+130^{\circ}=180^{\circ} \\ \Rightarrow \angle 1=180^{\circ}-130^{\circ} \\ \Rightarrow \angle 1=50^{\circ}
अतः \angle 1=50^{\circ}, \angle 4=130^{\circ}
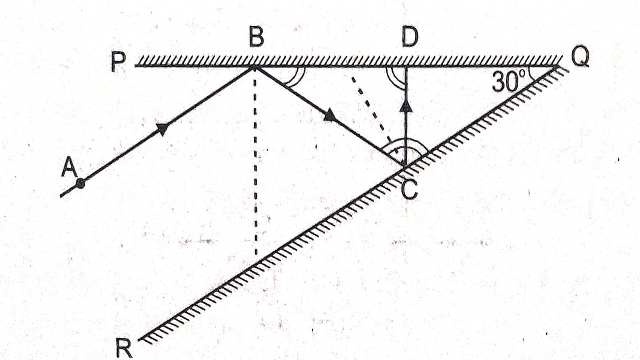
Example-9.चित्र में PQ एवं QR दो समतल दर्पण एक-दूसरे के साथ Q पर 30° कोण बनाते हुए जुड़े हुए हैं।आपतित किरण AB दर्पण RC के समान्तर हैं तो \angle BCQ,\angle CBQ तथा \angle BDC  का मान बताइए।

Solution–BL \perp PQ तथा CM \perp QR खींचा।
माना \angle ABC=2\angle x \\  \angle ABC=\angle CBL=\angle x
(आपतन कोण तथा परावर्तन कोण बराबर होते हैं)
A B \parallel R C \\ \angle A B Q+\angle B Q R=180^{\circ} (अन्त: कोणों का योग)

\Rightarrow \angle A B C+\angle Q B C+30^{\circ}=180^{\circ} \\ \Rightarrow 2 \angle x+\angle Q B C =180^{\circ}-30^{\circ} \\ \Rightarrow \angle x+\angle x+\angle Q B C=150^{\circ} \\ \Rightarrow \angle x+90^{\circ}=150^{\circ}
(BL,PQ पर लम्ब है)

\Rightarrow \angle x=150^{\circ}-90^{\circ} \\ \Rightarrow \angle x=60^{\circ} \\ \angle C B Q+\angle C B L=90^{\circ} \\ \angle C B Q+\angle x=90^{\circ} \\ \angle C BQ+60^{\circ}=90^{\circ} \\ \Rightarrow \angle CBQ=90^{\circ}- 60^{\circ} \\ \Rightarrow \angle C B Q=30^{\circ}
\triangle BCQ में

\angle C B Q+\angle B Q R+\angle B C Q=180^{\circ} \\ 30^{\circ}+30^{\circ}+\angle B C Q=180^{\circ} \\ \Rightarrow \angle B C Q=180^{\circ}-60^{\circ} \\ \Rightarrow \angle BCQ=120^{\circ} \\ \angle MCQ=90^{\circ}
अतः \angle B C M=120^{\circ}-90^{\circ} \\ \Rightarrow \angle B C M=30^{\circ} \\ \angle B C D=2 \times 30^{\circ}=60^{\circ}
\triangle BDC में

\angle Q B C+\angle B D C+\angle B C D=180^{\circ} \\ 30^{\circ}+60^{\circ}+\angle B C D=180^{\circ} \\ \Rightarrow \angle B C D=180^{\circ}-90^{\circ} \\ \Rightarrow \angle B C D=90^{\circ}
अतः \angle B C Q=120^{\circ}, \angle C B Q=30^{\circ}, \angle B DC=90^{\circ}
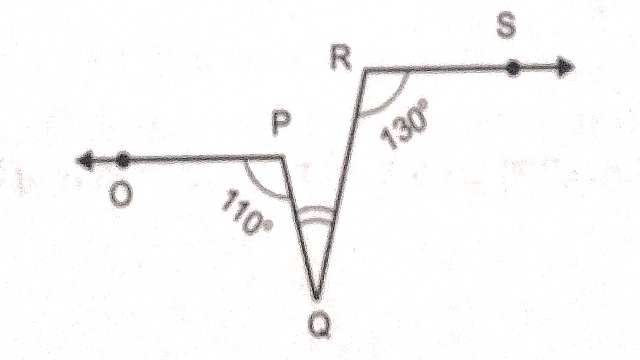
Example-10.चित्र में OP \parallel RS ; \angle OPQ=110^{\circ} और \angle QRS=130^{\circ} है तो \angle PQR बराबर है

Solution– PQ \parallel QY खींची
PQ \parallel RS तथा PQ \parallel QY
अतः RS \parallel QY
\angle SRX+\angle RQY=180^{\circ}(अन्त: कोणों का योग)
\Rightarrow 130^{\circ}+\angle RQY=180^{\circ} \\ \Rightarrow \angle RQY=180^{\circ}-130^{\circ} \\ \Rightarrow \angle RQY=50^{\circ} \\ PQ \parallel QY \\ \angle OPQ=\angle PQY(एकान्तर कोण)

\angle RQY=110^{\circ} \\ \Rightarrow \angle PQR + \angle RQY=110^{\circ} \\ \Rightarrow \angle PQR + 50^{\circ}=110^{\circ} \\ \Rightarrow \angle PQR=110^{\circ}-50^{\circ} \\ \Rightarrow \angle PQR=60^{\circ}
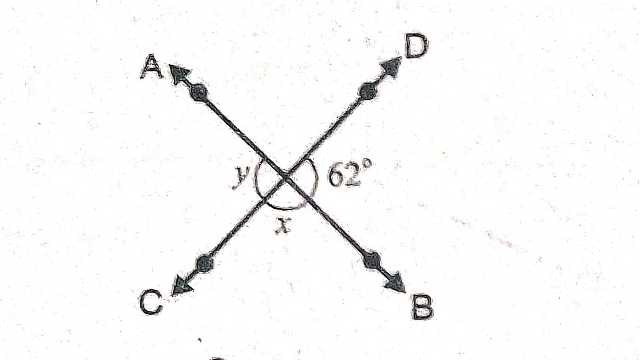
Example-11.चित्र में दो सरल रेखाएं AB तथा CD एक-दूसरे को O बिन्दु पर प्रतिच्छेद कर रही हैं और इस प्रकार बिन्दु O पर बने कोण अंकित हैं। \angle x- \angle y का मान है:

Solution–\angle x+62^{\circ}=180^{\circ}(रैखिक कोण युग्म)
\Rightarrow \angle x=180^{\circ}-62^{\circ} \\ \Rightarrow \angle x=118^{\circ} \\ \angle y=62^{\circ}(शीर्षाभिमुख कोण)

\angle x- \angle y=118^{\circ}-62^{\circ} \\ \Rightarrow \angle x- \angle y=56^{\circ}
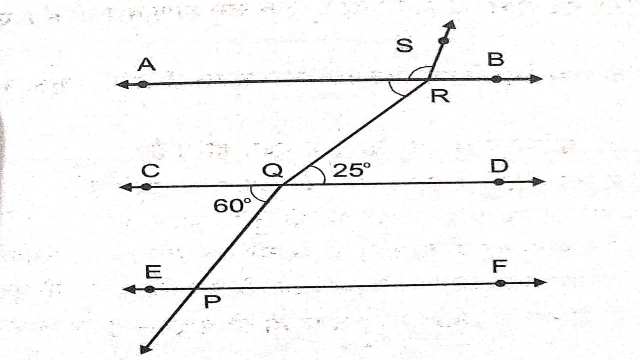
Example-12.चित्र में यदि AB \parallel CD \parallel EF,PQ\parallel RS ,\angle RQD=25^{\circ} और \angle CQP=60^{\circ} है तो \angle QRS बराबर है:

Solution–AB \parallel CD \parallel EF
अतः \angle PQC+ \angle ARS=180^{\circ} (रैखिक कोण युग्म से)
\Rightarrow 60^{\circ}+\angle ARS=180^{\circ} \\ \Rightarrow \angle ARS=180^{\circ}-60^{\circ} \\ \Rightarrow \angle ARS=120^{\circ} \\ \Rightarrow \angle ARQ=\angle RQD (एकान्तर कोण)

\angle ARQ=25^{\circ} \\ \angle QRS= \angle ARQ+\angle ARS \\ \Rightarrow \angle QRS=25^{\circ}+ 120^{\circ} \\ \Rightarrow \angle QRS=145^{\circ}
उपर्युक्त उदाहरणों के द्वारा समतल ज्यामिति परिचय एवं रेखाएं तथा कोण (Plane Geometry and Line and Angle) को समझ सकते हैं।

3.समतल ज्यामिति परिचय एवं रेखाएं तथा कोण की समस्याएं (Plane Geometry and Line and Angle Problems)-

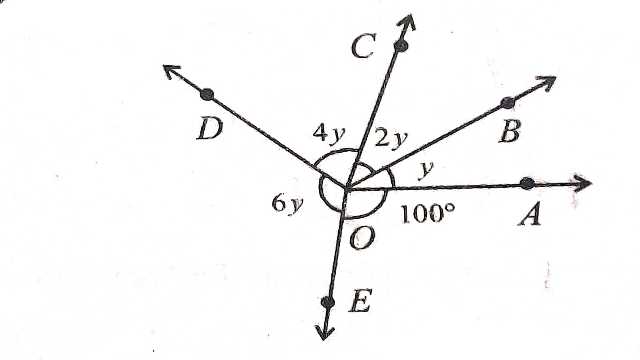
(1.)चित्र से कोण \angle AOB,\angle BOC,\angle COD तथा \angle DOE के माप ज्ञात कीजिए जहां \angle AOE=100^{\circ} है।

(2.)चित्र से \angle x, \angle y एवं \angle z के माप ज्ञात कीजिए।

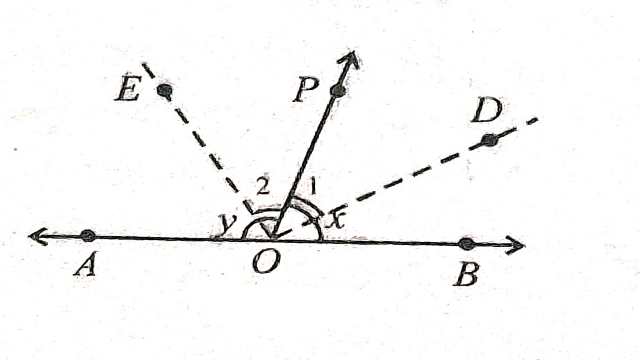
(3.)चित्र में AB एक रेखा है इससे दूसरी रेखा OP, बिन्दु O पर मिल रही है।रेखाएं OD तथा OE क्रमशः कोण \angle BOP और \angle POA के समद्विभाजक है। \angle EOD का मान ज्ञात कीजिए।

(4.)चित्र में BA \parallel ED  और BC \parallel EF हैं दर्शाइए कि \angle ABC=\angle DEF है।

उत्तर (Answers):(1)\angle AOB=20^{\circ},\angle BOC=40^{\circ},\angle COD=80^{\circ},\angle DOE=120^{\circ} \\ (2)\angle x=40^{\circ},\angle y=140^{\circ},\angle z=40^{\circ} \\ (3) \angle EOD=90^{\circ}
उपर्युक्त सवालों को हल करने पर समतल ज्यामिति परिचय एवं रेखाएं तथा कोण (Plane Geometry and Line and Angle) को ठीक से समझ सकते हैं।

4.समतल के लिए ज्यामितीय पद क्या है? (What is the geometric term for plane?)-

गणित में, एक समतल एक सपाट, दो आयामी सतह है जो असीम रूप से दूर तक फैली हुई है।एक समतल एक बिंदु (शून्य आयाम), एक रेखा (एक आयाम) और तीन आयामी स्थान का दो आयामी एनालॉग है।

5.क्या समतल ज्यामिति ज्यामिति के समान है? (Is plane geometry the same as geometry?)-

ज्यामिति में “समतल” बिना किसी मोटाई के समतल सतह होती है।लेकिन एक “मैदान” भूमि का एक बेतरतीब ज्यादातर सपाट विस्तार है जो सभी दिशाओं में अंतहीन रूप से फैला हुआ है।यह सपाट भी है,लेकिन उस शुद्ध अर्थ में नहीं जिसका हम उपयोग करते हैं …
(पढ़ें “कोण”)।शीर्ष हमेशा मध्य अक्षर होता है,के रूप में या बस लिखा जा सकता है।समतल-एक सपाट सतह जो सभी दिशाओं में अंतहीन रूप से फैली हुई है।
दो सपाट सतह, एक रेखा के साथ जहां एक दूसरे में प्रवेश करती है।यदि दो समतल समानांतर नहीं हैं, तो वे कहीं-कहीं एक-दूसरे को काटेंगे।

6.लाइन और प्लेन में क्या अंतर है? (What is the difference between a line and a plane?)-

एक रेखा को दो बिंदुओं द्वारा परिभाषित किया गया है और इसे नीचे एक तीर के साथ दिखाया गया है।एक बिंदु में मिलने वाली दो लाइनों को इंटरसेक्टिंग लाइन्स कहा जाता है।एक समतल दो आयामों में असीम रूप से विस्तारित होता है।एक समतल का नाम समतल में तीन बिंदुओं द्वारा रखा गया है जो एक ही रेखा पर नहीं हैं।
रेखा एक एकल विमीय है जबकि एक समतल 2 Dimentional.Plane को एक पेपर शीट के रूप में माना जा सकता है।यह बहुत मोटी नहीं है, लेकिन इसकी लंबाई और चौड़ाई है।बिन्दु आयाम रहित है।रेखा का एक आयाम है।प्लेन के दो या तीन आयाम होते हैं और ठोस में 3 आयाम होते हैं।

7.आप ज्यामिति में एक समतल को कैसे हल करते हैं? (How do you solve a plane in geometry?)-

किसी भी संख्या के आयामों के यूक्लिडियन स्थान में, एक समतल विशिष्ट रूप से निम्नलिखित में से किसी एक से निर्धारित होता है:
तीन नाॅन-कोलिनियर पॉइंट (एक लाइन पर अंक नहीं)।
एक लाइन और एक बिंदु उस रेखा पर नहीं।
दो अलग-अलग लेकिन प्रतिच्छेदी रेखाएँ।
दो अलग लेकिन समानांतर रेखाएं।

8.आप अपने द्वारा उपयोग की जा रही इकाइयों के आधार पर एक खंड की अपनी लंबाई कैसे लिखते हैं? (How do you write your length of a segment based on what units you are using?)-

यहां हम एक लाइन-सेगमेंट की लंबाई को मापना सीखेंगे। चलो वहाँ एक … पैमाने को रेखा-खंड के साथ रखा जाता है A में अपना शून्य (0) चिह्न लगाते हैं।हम देखते हैं कि B पैमाने के 3 सेमी के निशान पर है।तो … क्षमता मापने के लिए इकाइयाँ …
यदि आप इस पर दो बिंदु A और B अंकित करते हैं और इस सेगमेंट को अलग से उठाते हैं, तो यह एक लाइन बन जाता है … एक लाइन सेगमेंट की लंबाई या तो मीट्रिक इकाइयों में मापी जा सकती है जैसे … आम तौर पर एक सेंटीमीटर का उपयोग करके छोटे लाइन सेगमेंट को मापा जाता है।

9.रेखा,किरण और कोण (Lines Rays and Angles)-

एक किरण एक रेखा का हिस्सा है।एक किरण का एक समापन बिंदु होता है और एक दिशा में हमेशा के लिए जारी रहता है।एक लाइन खंड एक लाइन का हिस्सा है।यह दो समापन बिंदुओं के बीच की रेखा का हिस्सा है।एक कोण दो किरणों या लाइन खंडों द्वारा बनता है जो एक समापन बिंदु साझा करते हैं, जिसे कहा जाता है।

10.क्या एक लाइन एक बहुभुज है? (Is a line a polygon?)-

कंप्यूटिंग में लाइन एक बहुभुज है,क्योंकि यह 3 या अधिक बिंदुओं से बना होता है,जो सीधी रेखाओं से जुड़ा होता है। ज्यामिति में बहुभुज की अधिकांश परिभाषाओं के अनुसार, बहुभुज 2-आयामी आकार हैं।

11.आप लाइन सेगमेंट और एंगल्स को कैसे माप सकते हैं? (How can you find the measures of line segments and angles?)-

बीजगणित में हमने समतुल्य समतल का उपयोग रेखांकन और समीकरणों को हल करने में किया।आप एक निर्देशांक समतल में लाइनों, रेखाखंडों, किरणों और कोणों को अंकित कर सकते हैं।बिंदु B में शीर्ष के साथ एक कोण बनाते हैं।आप एक लाइन खंड की लंबाई को मापने के लिए निर्देशांक समतल का उपयोग कर सकते हैं।
उपर्युक्त उदाहरणों, सवालों को हल करके तथा प्रश्नों के उत्तर द्वारा समतल ज्यामिति परिचय एवं रेखाएं तथा कोण (Plane Geometry and Line and Angle) को भली-भांति समझ सकते हैं।

Also Read This Article:-Inequalities of triangle class 9

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here