Trigonometric functions of two angles
1.दो कोणों के त्रिकोणमितीय फलन (Trigonometric functions of two angles,Trigonometric functions of sum and difference of two angles class 11)-
दो कोणों के त्रिकोणमितीय फलनों (Trigonometric functions of two angles,Trigonometric functions of sum and difference of two angles class 11) की थ्योरी उदाहरण सहित तथा सर्वसमिकाएं उससे पूर्व आर्टिकल में पोस्ट कर चुके हैं।
इसलिए आप दो कोणों के त्रिकोणमितीय फलन (Trigonometric functions of two angles,Trigonometric functions of sum and difference of two angles class 11) के बारे में थ्योरी व सर्वसमिका के बारे में जानना चाहते हैं तो आपको उस आर्टिकल को पढ़ना चाहिए।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।
यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Middle term of binomial expansion
2.दो कोणों के त्रिकोणमितीय फलन के उदाहरण (Trigonometric functions of two angles examples), कक्षा 11 के दो कोणों योग और अंतर के त्रिकोणमितीय फलन के उदाहरण (Trigonometric functions of sum and difference of two angles class 11 examples)-
Example-1\cos { \left( \frac { \pi }{ 4 } -x \right) } \cos { \left( \frac { \pi }{ 4 } -y \right) } -\sin { \left( \frac { \pi }{ 4 } -x \right) } \sin { \left( \frac { \pi }{ 4 } -y \right) } =\sin { \left( x+y \right) }
Solution-LHS=\cos { \left( \frac { \pi }{ 4 } -x \right) } \cos { \left( \frac { \pi }{ 4 } -y \right) } -\sin { \left( \frac { \pi }{ 4 } -x \right) } \sin { \left( \frac { \pi }{ 4 } -y \right) } \\ \Rightarrow \cos { \left( \frac { \pi }{ 4 } -x+\frac { \pi }{ 4 } -y \right) } \qquad [\because \cos { A } \cos { B } -\sin { A } \sin { B } =\cos { (A+B) } ]\\ \Rightarrow \cos { \left( \frac { \pi }{ 2 } -x-y \right) } \\ \Rightarrow \cos { \left( \frac { \pi }{ 2 } -(x+y) \right) } \\ \Rightarrow \sin { \left( x+y \right) } =RHS
Example-2.\sin ^{ 2 }{ 6x } -\sin ^{ 2 }{ 4x } =\sin { 2x } \sin { 10x }
Solution-\sin ^{ 2 }{ 6x } -\sin ^{ 2 }{ 4x } =\sin { 2x } \sin { 10x } \\ LHS=\sin ^{ 2 }{ 6x } -\sin ^{ 2 }{ 4x } \\ \Rightarrow \left( \sin { 6x } -\sin { 4x } \right) \left( \sin { 6x } +\sin { 4x } \right) \\ \Rightarrow 2\cos { \left( \frac { 6x+4x }{ 2 } \right) } \sin { \left( \frac { 6x-4x }{ 2 } \right) } .2\sin { \left( \frac { 6x+4x }{ 2 } \right) } \cos { \left( \frac { 6x-4x }{ 2 } \right) } \\ \Rightarrow 2\cos { 5x } \sin { x } .2\sin { 5x } \cos { x } \\ \Rightarrow (2\cos { 5x } \sin { 5x } )(2\sin { x } \cos { x } )\\ \Rightarrow \sin { 10x } \sin { 2x } =RHS
Example-3.\sin { 2x } +2\sin { 4x } +\sin { 6x } =4\cos ^{ 2 }{ x } \sin { 4x }
Solution–\sin { 2x } +2\sin { 4x } +\sin { 6x } =4\cos ^{ 2 }{ x } \sin { 4x } \\ LHS=\sin { 2x } +2\sin { 4x } +\sin { 6x } \\ \Rightarrow \sin { 2x } +\sin { 4x } +\sin { 4x } +\sin { 6x } \\ \Rightarrow 2\sin { \left( \frac { 2x+4x }{ 2 } \right) } \cos { \left( \frac { 4x-2x }{ 2 } \right) } +2\sin { \left( \frac { 6x+4x }{ 2 } \right) } \cos { \left( \frac { 6x-4x }{ 2 } \right) } \\ \Rightarrow 2\sin { 3x } \cos { x } +2\sin { 5x } \cos { x } \\ \Rightarrow 2\cos { x } \left[ \sin { 3x } +\sin { 5x } \right] \\ \Rightarrow 2\cos { x } \left[ 2\sin { \left( \frac { 3x+5x }{ 2 } \right) } \cos { \left( \frac { 5x-3x }{ 2 } \right) } \right] \\ \Rightarrow 2\cos { x } \left[ 2\sin { 4x } \cos { x } \right] \\ \Rightarrow 4\cos ^{ 2 }{ x } \sin { 4x }
Example-4.\frac { \sin { 5x } -2\sin { 3x } +\sin { x } }{ \cos { 5x } -\cos { x } } =\tan { x }
Solution–\frac { \sin { 5x } -2\sin { 3x } +\sin { x } }{ \cos { 5x } -\cos { x } } =\tan { x } \\ LHS=\frac { \sin { 5x } -2\sin { 3x } +\sin { x } }{ \cos { 5x } -\cos { x } } \\ \Rightarrow \frac { \sin { 5x } -\sin { 3x } -\sin { 3x } +\sin { x } }{ \cos { 5x } -\cos { x } } \\ \Rightarrow \frac { 2\cos { \left( \frac { 5x+3x }{ 2 } \right) } \sin { \left( \frac { 5x-3x }{ 2 } \right) } -(\sin { 3x } -\sin { x } ) }{ \cos { 5x } -\cos { x } } \\ \Rightarrow \frac { 2\cos { 4x } \sin { x } -2\cos { \left( \frac { 3x+x }{ 2 } \right) } \sin { \left( \frac { 3x-x }{ 2 } \right) } }{ \cos { 5x } -\cos { x } } \\ \Rightarrow \frac { 2\cos { 4x } \sin { x } -2\cos { \left( \frac { 3x+x }{ 2 } \right) } \sin { \left( \frac { 3x-x }{ 2 } \right) } }{ 2\sin { \left( \frac { 5x+x }{ 2 } \right) } \sin { \left( \frac { x-5x }{ 2 } \right) } } \\ \Rightarrow \frac { 2\cos { 4x } \sin { x } -2\cos { 2x } \sin { x } }{ 2\sin { 3x } \sin { \left( -2x \right) } } \\ \Rightarrow \frac { 2\sin { x } (\cos { 4x } -\cos { 2x } ) }{ 2\sin { 3x } \sin { \left( -2x \right) } } \\ \Rightarrow \frac { 2\sin { x } 2\sin { \left( \frac { 4x+2x }{ 2 } \right) } \sin { \left( \frac { 2x-4x }{ 2 } \right) } }{ -2\sin { 3x } \sin { 2x } } \\ \Rightarrow \frac { 4\sin { x } \sin { 3x } \sin { \left( -x \right) } }{ -2\sin { 3x } \sin { 2x } } \\ \Rightarrow \frac { -4\sin { x } \sin { 3x } \sin { x } }{ -2\sin { 3x } \sin { 2x } } \\ \Rightarrow \frac { 2\sin ^{ 2 }{ x } }{ \sin { 2x } } \\ \Rightarrow \frac { \sin { x } }{ \cos { x } } \\ \Rightarrow \tan { x } =RHS
Example-5.यदि \sin { (A+B) } =a तथा \cos { A } +\cos { B } =b हो तो सिद्ध कीजिए कि \cos { (A+B) } =\frac { { b }^{ 2 }-{ a }^{ 2 } }{ { a }^{ 2 }+{ b }^{ 2 } }
Solution-\sin { (A+B) } =a
वर्ग करने पर-\sin ^{ 2 }{ A } +\sin ^{ 2 }{ B } +2\sin { A } \sin { B } ={ a }^{ 2 }.........................(1) \\ \cos { A } +\cos { B } =b
वर्ग करने पर-\cos ^{ 2 }{ A } +\cos ^{ 2 }{ B } +2\cos { A } \cos { B } ={ b }^{ 2 }.......................(2)
समीकरण (2) में समीकरण (1) को जोड़ने पर-
\sin ^{ 2 }{ A } +\cos ^{ 2 }{ A } +\sin ^{ 2 }{ B } +\cos ^{ 2 }{ B } +2\sin { A } \sin { B } +2\cos { A } \cos { B } ={ a }^{ 2 }+{ b }^{ 2 }\\ \Rightarrow 1+1+2\sin { A } \sin { B } +2\cos { A } \cos { B } ={ a }^{ 2 }+{ b }^{ 2 }\\ \Rightarrow 2+2\sin { A } \sin { B } +2\cos { A } \cos { B } ={ a }^{ 2 }+{ b }^{ 2 }\\ \Rightarrow 2[1+\sin { A } \sin { B } +\cos { A } \cos { B } ]={ a }^{ 2 }+{ b }^{ 2 }\\ \Rightarrow 2[1+\cos { (A-B) } ]={ a }^{ 2 }+{ b }^{ 2 }...............(3)
समीकरण (2) में समीकरण (1) को घटाने पर-
-\sin ^{ 2 }{ A } +\cos ^{ 2 }{ A } -\sin ^{ 2 }{ B } +\cos ^{ 2 }{ B } +2\cos { A } \cos { B } -2\sin { A } \sin { B } ={ b }^{ 2 }-{ a }^{ 2 }\\ \Rightarrow -(1-\cos ^{ 2 }{ A } )+\cos ^{ 2 }{ A } -\sin ^{ 2 }{ B } +(1-\sin ^{ 2 }{ B } )+2\cos { A } \cos { B } -2\sin { A } \sin { B } ={ b }^{ 2 }-{ a }^{ 2 }\\ \Rightarrow -1+\cos ^{ 2 }{ A } +\cos ^{ 2 }{ A } +1+\sin ^{ 2 }{ B } +\sin ^{ 2 }{ B } +2(\cos { A } \cos { B } -\sin { A } \sin { B } )={ b }^{ 2 }-{ a }^{ 2 }\\ \Rightarrow 2\cos ^{ 2 }{ A } -2\sin ^{ 2 }{ B } +2\cos { (A+B) } ={ b }^{ 2 }-{ a }^{ 2 }\\ \Rightarrow 2(\cos ^{ 2 }{ A } -\sin ^{ 2 }{ B } )+2\cos { (A+B) } ={ b }^{ 2 }-{ a }^{ 2 }\\ \Rightarrow 2 \cos (A+B) \cos (A-B) +2 \cos (A+B) =b^{ 2 }-a^{ 2 }
\left[ \because \cos ^{ 2 }{ A } -\sin ^{ 2 }{ B } =\cos (A+B) \cos (A-B) \right]
\Rightarrow 2 \cos { (A+B) } [1+\cos { (A-B) } ]={ b }^{ 2 }-{ a }^{ 2 }..............(4)
समीकरण (4) में समीकरण (3) का भाग देने पर-
\cos { (A+B) } =\frac { { b }^{ 2 }-{ a }^{ 2 } }{ { b }^{ 2 }+{ a }^{ 2 } }
उपर्युक्त उदाहरणों के द्वारा दो कोणों के त्रिकोणमितीय फलन (Trigonometric functions of two angles,Trigonometric functions of sum and difference of two angles class 11) को समझा जा सकता है।
3.दो कोणों के त्रिकोणमितीय फलन की समस्याएं (Trigonometric functions of two angles Problems),कक्षा 11 के दो कोणों योग और अंतर के त्रिकोणमितीय फलन के समस्याएं (Trigonometric functions of sum and difference of two angles class 11 Problems)-
(1)\cot { 4x } (\sin { 5x } +\sin { 3x } )=\cot { x } (\sin { 5x } -\sin { 3x } )\\ (2)\frac { \sin { x } +\sin { 3x } }{ \cos { x } +\cos { 3x } } =\tan { 2x } \\ (3)\frac { \sin { x } -\sin { y } }{ \cos { x } -\cos { y } } =\tan { \left( \frac { x-y }{ 2 } \right) } \\ (4)[1+\cot { \theta } -\sec { \left( \theta +\frac { \pi }{ 2 } \right) } ][1+\cot { \theta } +\sec { \left( \theta +\frac { \pi }{ 2 } \right) } ]=2\cot { \theta } \\ (5)\cos { 4x } =1-8\sin ^{ 2 }{ x } \cos ^{ 2 }{ x } \\ (6)\frac { \cos { 4x } +\cos { 3x } +\cos { 2x } }{ \sin { 4x } +\sin { 3x } +\sin { 2x } } =\cot { 3x }
उपर्युक्त समस्याओं को हल करने पर दो कोणों के त्रिकोणमितीय फलन (Trigonometric functions of two angles,Trigonometric functions of sum and difference of two angles class 11) ओर अधिक ठीक से समझ में आ जाएगा।
4.डबल एंगल फॉर्मूला किसके लिए प्रयोग किया जाता है? (What is the double angle formula used for?)-
कोसाइन डबल कोण सूत्र हमें बताता है कि cos (2θ) हमेशा cos²θ-sin²θ के बराबर होता है।उदाहरण के लिए cos (60), cos²(30)-sin²(30)) के बराबर है। हम इस पहचान का उपयोग अभिव्यक्ति को फिर से लिखने या समस्याओं को हल करने के लिए कर सकते हैं।
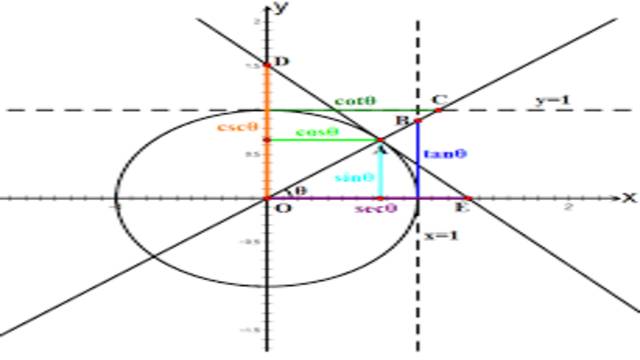
5.एक कोण के छह वृत्तीय फलन क्या हैं? (What are the six circular functions of an angle?)-
प्री-कैलकुलस में, आपको यूनिट सर्कल पर सिंगल एंगल के लिए छह त्रिकोणमितीय फंक्शंस – साइन, कॉसिन, टेंजेंट, कोसेकेंट, सेकेंट और कॉटेजेंट – का मूल्यांकन करने की आवश्यकता होती है।यूनिट सर्कल पर प्रत्येक कोण के लिए, तीन अन्य कोणों में समान त्रिकोणमितीय फ़ंक्शन मान होते हैं।
6.विशेष कोणों के त्रिकोणमितीय फलन क्या हैं? (What are the trigonometric functions of special angles?)-
आपको कुछ विशेष कोणों के फ़ंक्शन मानों को जानना होगा, अर्थात् 30 ° (π / 6), 45 ° (π/4), और 60 ° (π / 3)।आपको पीछे जाने में सक्षम होने और यह जानने की भी आवश्यकता है कि sine में ½ या टेंजेंट में −√3 किस कोण का मान है।
उपर्युक्त प्रश्नों के उत्तर द्वारा दो कोणों के त्रिकोणमितीय फलनों (Trigonometric functions of two angles,Trigonometric functions of sum and difference of two angles class 11) ओर क्लीयर हो जाएगा।
Also Read This Article:-Sum of first n term of an AP
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |