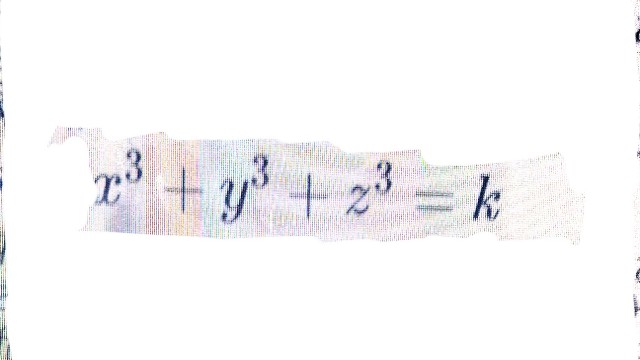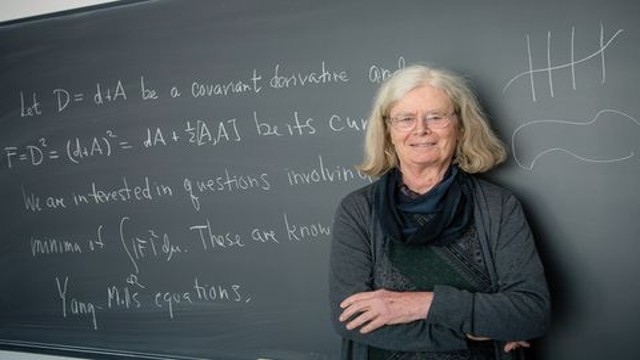10 Biggest Math Breakthroughs of 2019
2019 की 10 सबसे बड़ी गणित सफलता का परिचय(Introduction to 10 Biggest Math Breakthroughs of 2019):
- 2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019) के बारे में बताया गया है जो बहुत समय से गणितज्ञों के लिए समस्या बनी हुई थी। हालांकि इनमें नवीन समस्याएं भी शामिल हैं। इनमें 2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019) में से कुछ को सुलझा लिया गया है जबकि कुछ को कुछ हद तक सुलझा लिया गया है।
- इन 2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019) के आधार पर यह कहा जा सकता है कि वर्ष 2019 गणितज्ञों के लिए बहुत शुभ तथा अच्छा रहा है।
- ये 10 गणित की अनसुलझी समस्याएं गणितज्ञों के लिए काफी समय से समस्या बनी हुई थी। परन्तु गणितज्ञों के जीवट,समर्पण,कड़ी मेहनत के सामने इन समस्याओं को हार मानना पड़ा।इस प्रकार जिन गणितज्ञों का 2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019) में योगदान रहा है उनको साधुवाद।
इन महान गणितज्ञों की वजह से ही गणित विषय नवीन और प्रगतिशील बना रहता है। गणित विषय को रोचक,सरल तथा उपादेय बनाने के लिए इन सभी गणितज्ञों का महान् योगदान है। - इन सभी 2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019) का वर्णन क्रमशः इस आर्टिकल में किया गया है।यदि यह आर्टिकल एक बार पढ़ने से समझ में न आए तो इसे दुबारा पढ़े। निश्चित रूप से आपके यह आर्टिकल समझ में आ जाएगा।
- हर वर्ष महान् गणितज्ञों द्वारा सदियों पुरानी अनसुलझी समस्याओं का समाधान करते रहते हैं। इसके साथ-साथ नई-नई समस्याओं का भी समाधान करते हैं।इस कारण गणित विषय जीवंत बना रहता है। गणित विषय की इन्हीं खूबियों के कारण नई-नई प्रतिभाएं गणित विषय की ओर आकर्षित होती है। इस प्रकार गणित में ये प्रतिभाएं अपना कुछ न कुछ योगदान देकर गणित विषय को समृद्ध, विकसित तथा उन्नत करती रहती है।
- हालांकि ओर भी कई गणितीय समस्याओं का समाधान 2019 में हुआ है। परन्तु हमने इस आर्टिकल में सबसे अधिक महत्त्वपूर्ण गणितीय समस्याओं को ही शामिल किया है।
- आप भी 2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019) को पढ़कर इसका आनन्द उठाएं।इस प्रकार की गणितीय समस्याएं हमें रोमांचित तथा आकर्षित करती रहती है।
- 2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019) को पढ़कर हम यह समझ लेते हैं कि यह तो सामान्य बात है।परन्तु इन समस्याओं को हल करने में इन महान् गणितज्ञों को कितना परिश्रम तथा त्याग करना पड़ता है,इसे वे ही जान सकते हैं।इन गणितज्ञों के इस त्याग और तपस्या को नमन है जिन्होंने गणित की समस्याओं का समाधान किया है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019):
- { x }^{ 3 }+{ y }^{ 3 }+{ z }^{ 3 }
प्राचीन सवालों के जवाब देने से लेकर नए नवाचारों को खोजने तक, ये साल की शानदार गणितीय हाइलाइट हैं।
2019 में, गणित में कई मुख्यधारा के क्षण थे – और यह उन वायरल समस्याओं को शामिल नहीं करता था जो हमें हमारे बालों को चीरना चाहते थे। इस साल ने कठिन सवालों के जवाब (या कम से कम आंशिक उत्तरों) की एक स्थिर धारा देखी, जो दशकों से गणितज्ञों को हैरान कर रहे थे, साथ ही साथ नई तकनीकों ने भी हमारा ध्यान बड़े पैमाने पर खींचा। यहाँ संख्याएँ हैं – और उनके पीछे दिमाग – जो इस साल सबसे ज्यादा मायने रखता है
Also Read This Article:-Award to Indian origin’s mathematicians
1.रीमैन हाइपोथीसिस पर प्रोग्रेस (Progress on the Riemann Hypothesis):
- रीमैन हाइपोथीसिस को आमतौर पर वर्तमान गणित में सबसे बड़ी खुली समस्या के रूप में देखा जाता है। 1859 के बाद से, यह संबंधित है कि कैसे अभाज्य संख्याएँ काम करती हैं, और गणित की कई अन्य शाखाओं से जुड़ती हैं। शोधकर्ताओं ने इस वर्ष सीधे रीमैन परिकल्पना से संबंधित कुछ साबित किया। उनका प्रमाण दोनों बड़े प्रश्न को हल करने के लिए व्यावहारिक है, और अपने आप में आकर्षक है।
2. तीन घन का योग (The Sum of Three Cubes):
- { x }^{ 3 }+{ y }^{ 3 }+{ z }^{ 3 }=k\\ k=42
- यह कुछ गंभीर रूप से प्राचीन गणित है। डायोफैंटाइन समीकरणों का नाम अलेक्जेंड्रिया के डायोफैंटस के नाम पर रखा गया है, जो तीसरी शताब्दी के गणितज्ञ हैं। इस फोटो में देखे गए दो विशेष डायोफैंटाइन समीकरणों ने 2019 तक गणितज्ञों को विकसित किया। साझा कंप्यूटर शक्ति में नवीनतम तकनीक द्वारा सफलता को सक्षम किया गया था।
3. कोलेट्ज अनुमान (The Collatz Conjecture):
- f\left( n \right) =\left\{ \begin{matrix} \frac { n }{ 2 } \quad \quad \quad if\quad n\quad is\quad even \\ 3n+1\quad if\quad n\quad is\quad odd \end{matrix} \right\}
- गणित की सबसे बड़ी खुली समस्याओं में से एक इस साल एक संकल्प के करीब कूद गई। विपुल गणितज्ञ टेरेंस ताओ द्वारा पोस्ट किए गए बेहतर परिणामों ने गणित समुदाय को हिला दिया। डॉ. ताओ की नवीनतम जानकारियों के बाद भी, समस्या अधूरी है, और हल होने में अभी भी कई साल लग सकते हैं।
4.संवेदनशीलता का अनुमान (The Sensitivity Conjecture):
- computational proof of Huang’s degree theorem
(Don Knuth, Stanford Computer Science Department; 28 July 2019, revised 3 August 2019)
that establishes Nisan and - Hao Huang recently posted his proof [1] of a beautiful combinatorial theorem Szegedy’s 30-year-old Sensitivity Conjecture for Boolean functions:
Theorem. Any set H of { 2 }^{ n-1 }+1vertices of the n-cube contains a vertex with at least \sqrt { n } neighbors in H.
His proof used the interesting sequence of symmetric { 2 }^{ n }\times { 2 }^{ n } matrices A, defined recursively by - { A }_{ 0 }=\left( 0 \right) ,\quad \quad { A }_{ n }=\begin{pmatrix} { A }_{ n-1 } & { I }_{ { 2 }^{ n-1 } } \\ { I }_{ { 2 }^{ n-1 } } & { -A }_{ n-1 } \end{pmatrix},\quad for\quad n>0
- An easy induction proves that { A }_{ n }^{ 2 }=n{ I }_{ { 2 }^{ n } } for all n\ge 0. Furthermore, every row and column of { A }_{ n } has exactly n nonzero entries. Indeed, if we number the rows and columns in binary notation from 0…0 to1 .. .1, the entry in row \alpha ={ a }_{ 1 }..........{ a }_{ n } and column \beta ={ b }_{ 1 }...........{ b }_{ n } is \pm 1 when \left| { a }_{ 1 }-{ b }_{ 1 } \right| +.............+\left| { a }_{ n }-{ b }_{ n } \right| =1.otherwise it is zero.
Now let { B }_{ n } be the { 2 }^{ n }\times { 2 }^{ n-1 } matrix - { B }_{ n }=\left( \begin{matrix} { A }_{ n-1 }+\sqrt { n } { I }_{ { 2 }^{ n-1 } } \\ { I }_{ { 2 }^{ n-1 } } \end{matrix} \right)
Then B. has rank { 2 }^{ n-1 }, and we have
{ A }_{ n }{ B }_{ n }=\left( \begin{matrix} { { A }_{ n-1 }^{ 2 }+\sqrt { n } A }_{ n-1 }+{ I }_{ { 2 }^{ n-1 } } \\ { \sqrt { n } I }_{ { 2 }^{ n-1 } } \end{matrix} \right) =\left( \begin{matrix} { \sqrt { n } A }_{ n-1 }+{ I }_{ { 2 }^{ n-1 } } \\ { \sqrt { n } I }_{ { 2 }^{ n-1 } } \end{matrix} \right) =\sqrt { n } { B }_{ n } - 1994 में हुआ, संवेदनशीलता का अनुमान गणितीय कंप्यूटर विज्ञान में एक प्रमुख अनसुलझा प्रश्न बन गया। यह इस वर्ष समाप्त हो गया, इमोरी विश्वविद्यालय के प्रोफेसर हाओ हुआंग के लिए धन्यवाद। प्रारंभिक घोषणा के बाद कुछ हफ़्ते में, वैज्ञानिकों ने डॉ. हुआंग के प्रमाण को एक पृष्ठ के प्रतिभाशाली तक पचा लिया।
5.कैंसर अनुसंधान के लिए एक महान वर्ष (A Great Year for Cancer Research):
- गणितज्ञ हमेशा कैंसर के खिलाफ लड़ाई में मदद करने के तरीकों की तलाश में रहते हैं।वर्ष की शुरुआत गणितज्ञों और द्वारा इस संयुक्त कार्य के साथ की गई थी।अभिनव गणित मॉडलिंग ने सेल के विकास पर अपने प्रयोगों को निर्देशित करने में मदद की। फिर यह शोध आया, जिसने स्तन कैंसर के मेटास्टेसिस के बारे में नई जानकारी हासिल करने के लिए गणित के मॉडल का इस्तेमाल किया।
6.किरिगामी गणित हो जाता है (Kirigami Gets Mathematized):
- किरिगामी, जिसका अर्थ है “पेपर कटिंग,” ओरिगामी (“पेपर फोल्डिंग”) की तुलना में कम प्रसिद्ध है, लेकिन दोनों औद्योगिक अनुप्रयोगों में अपनी पसंद पा रहे हैं। हार्वर्ड के शोधकर्ताओं ने इस साल किरिगामी के गणित में महारत हासिल की, विनिर्माण और सामग्री विज्ञान में नए मोर्चे को रोशन किया।
7. सूरजमुखी अनुमान (The Sunflower Conjecture):
- दशकों की निष्क्रियता के बाद, 2019 ने सनफ्लॉवर अनुमान पर प्रगति देखी, जो 1960 में पॉल एर्दो के गणित के दुनिया के सबसे प्रसिद्ध और रंगीन पात्रों में से एक था। नई जानकारी पिछले ज्ञान से एक बड़ा कदम है, लेकिन अभी भी एर्दो के मूल प्रश्न का पूरी तरह से जवाब नहीं है।
8. रैम्सी सिद्धांत में एक सफलता (A Breakthrough in Ramsey Theory):
- रैमसे थ्योरी में, गणितज्ञ बड़ी मात्रा में अराजकता के बीच पूर्वानुमेय पैटर्न की तलाश करते हैं। 1969 के एक सवाल का आखिरकार इस साल जवाब दिया गया, और इसके शोधकर्ताओं ने इसे एक आसान सादृश्य के साथ वर्णित किया: “कभी जीतने वाली लॉटरी टिकट।”
9.नया द्विघात सूत्र (New Quadratic Formula):
- x=\frac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }
- कार्नेगी मेलन विश्वविद्यालय के प्रोफेसर पो-शेन लोह ने इस वर्ष लहरें बनाईं, जो द्विघात समीकरणों के निकट आने के वैकल्पिक तरीके को लोकप्रिय बनाता था। लोह बताते हैं कि उनके द्वारा इस्तेमाल किया गया गणित सदियों से जाना जाता है, लेकिन उनका वर्णनात्मक दृष्टिकोण ताज़ा है, और द्विघात समीकरणों को सीखने वाले छात्रों की नई पीढ़ियों के लिए बेहतर साबित हो सकता है।
10. सबसे अच्छे गणितज्ञ अंत में ताज पहनाया जाता है (The Coolest Mathematician Finally Gets Crowned):
- डॉ. करेन उहलेनबेक (Karen Uhlenbeck) ने अपने दशकों के जबरदस्त काम के लिए, गणित के सर्वोच्च सम्मानों में से एक, इस साल का एबेल पुरस्कार अर्जित किया। डॉ. उहलेनबेक ने शाब्दिक रूप से पुस्तकों को भरने के लिए पर्याप्त गणित का आविष्कार किया। ज्यामितीय विश्लेषण और गेज सिद्धांत जैसे कुछ सुपर उन्नत गणित विषयों में उसका नाम सबसे आगे है।
उपर्युक्त 2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019) हैं।
Also Read This Article:-Abel Prize was given two mathematician
10 Biggest Math Breakthroughs of 2019
2019 की 10 सबसे बड़ी गणित सफलता
(10 Biggest Math Breakthroughs of 2019)
10 Biggest Math Breakthroughs of 2019
2019 की 10 सबसे बड़ी गणित सफलता (10 Biggest Math Breakthroughs of 2019)
के बारे में बताया गया है जो बहुत समय से गणितज्ञों के लिए समस्या बनी हुई थी। हालांकि इनमें नवीन समस्याएं भी शामिल हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |
No Responses